在民用飞机总体设计及功能要求中,一般需要在机身上布置较多的舱门,比如应急门、登机门、货舱门和机组逃生门等等,因此在机身形成较多开口区域。由于机身舱门开口区域较大,导致结构以及传力发生很大变化,具体为：(1) 结构的刚度发生突变,变形不连续;(2) 破坏了机身结构的连续性以及原有结构的传力路线,载荷的传递发生变化;(3) 加强开口区域结构以承受原开口处壁板所承受的载荷以及载荷的重新分布而引起的附加载荷,必然增大结构的重量^[1-2]。因此,在机身强度设计时除了确定蒙皮、长桁、框等常规的结构尺寸外,在满足其他功能要求前提下,确定开口区域的最优开口大小以及加强结构尺寸成为机身设计的重点和难点。

目前飞机机身开口结构的设计及分析主要采用数值计算结合有限元分析方法,主要针对飞机结构详细设计阶段^[3-6],但是在飞机结构初步设计阶段没有足够的结构参数来建立有限元模型。本文从机身开口结构的工程分析方法出发,通过对机身开口结构的弯曲刚度特性进行研究,得到机身开口结构刚度的主要参数的影响,提出开口加强的原则和方法,确定开口区域的最优开口大小以及加强结构初步尺寸,该方法对于飞机结构初步设计阶段机身开口结构设计具有一定的参考意义。

对于机身开口区域的设计,最基本的要求就是保证载荷的传递,使结构满足规定的刚度和强度要求^[7]。从刚度角度考虑,要求机身开口区变形协调,满足一定变形要求,同时开口区变形不影响飞机其他功能的实现,比如舱门的开启或关闭等。从强度角度考虑,要求应力分布合理,没有明显的应力集中,结构本体及其连接能够满足强度要求,即受拉不破坏,限制载荷范围内受压、受剪不失稳^[8]。

机身结构开口后,剖面形心、惯性矩和静矩等物理量都发生了变化,导致应力数值和分布发生变化。机身开口大小直接影响机身的刚度和强度,因此,通过对机身开口区刚度和强度计算及分析研究,可以较准确地确定相关影响因素,得到最优开口大小以及加强结构尺寸,进一步明确结构设计加强的方向和方法,从而确定该类型结构设计的总体方案。

刚度是指外力作用下,结构抵抗变形的能力。结构刚度取决于结构材料的性能和结构的几何尺寸。对于机身结构而言,一般选用铝合金,因此,应该通过设计结构的尺寸来满足刚度设计要求^[9]。

2.1.1 机身开口区刚度计算模型简化

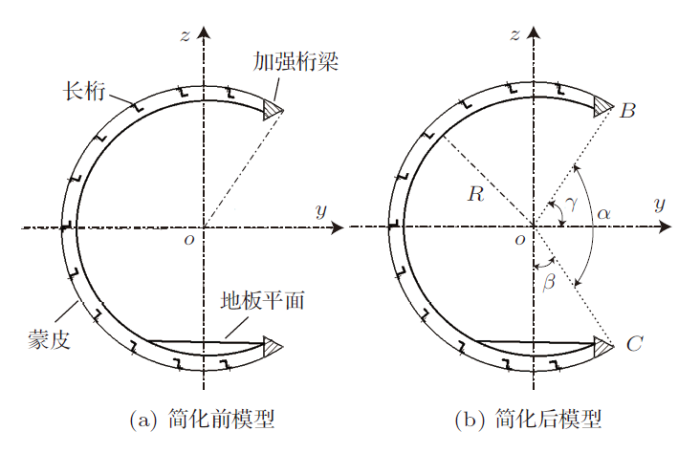
对机身开口区刚度进行分析计算时首先对开口区截面进行模型简化,开口区简化计算模型如图1所示,图1(b)中$R$为机身半径,$\gamma$为开口区上部点$B$与圆心连线与$z$轴夹角,$\beta$为开口区下部点$C$与圆心连线与$z$轴夹角,$\alpha$为开口角度。机身开口区下部点$C$为地板平面与开口区截面的交点,此点为固定点。根据机身地板平面高度与截面尺寸可以求出$\beta$。

首先是蒙皮的折算,相关研究资料仅将长桁截面积折算到蒙皮上,没有考虑隔框的面积^[10]。本文计算时将长桁及隔框的横截面面积折算到蒙皮厚度中

式中, $\delta_{0} $为蒙皮的折算厚度;$\delta_{\rm mp}$为蒙皮初始厚度;$S_{\rm ch}$为长桁间距;$F_{\rm ch}$为长桁的横截面面积;$S_{\rm gk}$为隔框间距;$F_{\rm gk} $为隔框的横截面面积。

2.1.2 刚度计算

根据2.1.1节简化模型及机身开口区的受力特点,对开口区垂向弯曲刚度即机身开口结构剖面相对于形心轴的惯性矩进行计算。

首先计算简化模型关于$y$轴的静矩

式中, $z$为简化后截面面积$Z$坐标值;$A_i $为开口处上下加强桁梁的面积;$z_i$为上下加强桁梁$Z$坐标值;$A_{\rm jq}$为开口处加强桁梁的实际面积。

简化模型截面面积$A$为

则形心垂向位置$z_{\rm c}$为

开口模型关于$y$轴的惯性矩$I_y$为

根据材料力学中平行移轴公式,该剖面相对于形心轴的惯性矩$I_{y \rm c}$为

式中

令开口区开口角度$\alpha = \dfrac{1}{2}\pi - \beta +\gamma$。 从式(6)$\sim$式(8)可以看出, 开口模型的垂向弯曲刚度与开口角度$\alpha$以及$\dfrac{A_{\rm jq}}{R\delta_0}$有关。

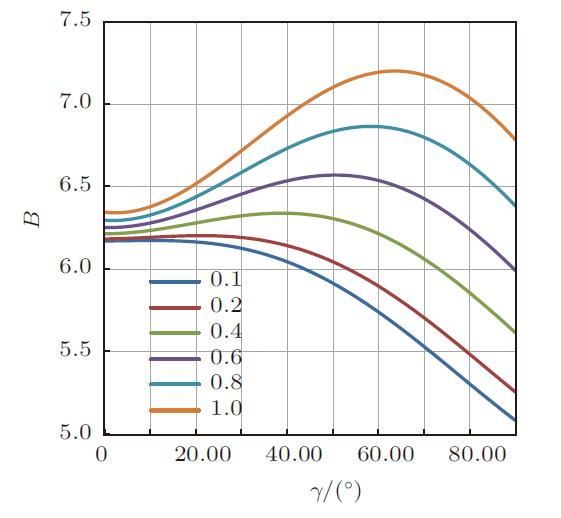
在飞机总体布置下,地板平面位置确定后,舱门开口下部点就可以确认,即$\beta$为确定值。根据2.1.2节刚度计算得到的垂向弯曲刚度系数的表达式 (7)和式(8),令该系数为$B= B_1 + B_2 $, 此系数为一无量纲数值。 在一系列$\dfrac{A_{jq} }{R\delta _0}= (0.1$,0.2,0.4,0.6,0.8,1.0)下,可以计算出分别对应不同$\gamma$下垂向弯曲刚度系数$B$,变化曲线如图2所示。设计中可根据总体刚度要求并结合图2曲线和合理选择开口角度$\alpha$及$\dfrac{A_{jq} }{R\delta _0 }$。

从图2中可以看出,垂向弯曲刚度先增大后减小,原因为：当开口角度较小时,随着开口角度增大,上部加强桁梁的位置也随着增高,加强桁梁垂向弯曲刚度增大,由于开口角度较小加强桁梁垂向弯曲刚度增加量大于结构开口引起刚度减小量,整体结构弯曲刚度增大;当开口角度进一步增大后,结构开口引起的刚度减小量大于加强桁梁垂向弯曲刚度增加量,整体结构弯曲刚度减小。

2.1.3 模型验证

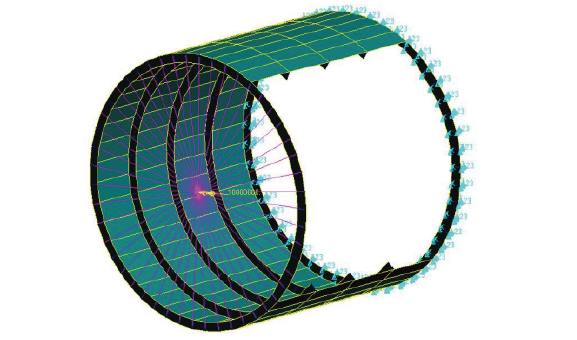
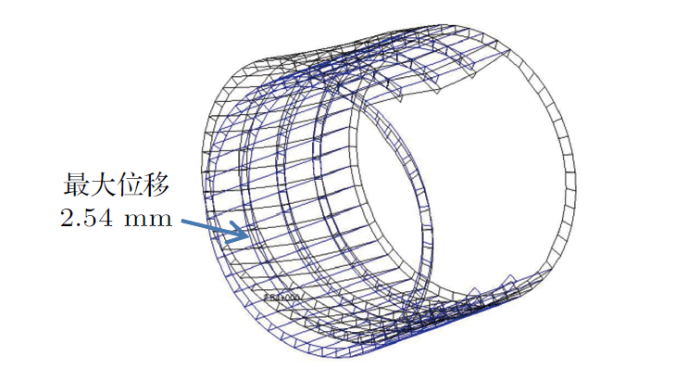
本节将应用有限元计算结果对上述模型简化及计算方法进行验证。假设机身半径$R$为1025 mm, $\gamma$为55$^\circ $,$\beta $为42$^\circ$,蒙皮厚度$\delta_{\rm mp}$为2 mm, 长桁间距$S_{\rm ch}$为140 mm$^{2}$,长桁的横截面面积$F_{\rm ch}$为100 mm$^2$,隔框间距$S_{\rm gk}$为430 mm,隔框的横截面面积$F_{\rm gk}$ 为100 mm$^{2}$,开口处加强桁梁的面积$A_{\rm jq}$为100 mm$^{2}$。通过以上数据建立如图3所示的开口筒段有限元模型,开口模型一端将三个方向位移约束,另一端施加大小为10$^{9}$ N$\cdot$mm的垂向弯矩,开口筒段长为1720 mm。经过计算可以得到图4 所示有限元位移计算结果,最大位移为2.54 mm。

在相同尺寸及载荷工况下,根据2.1.2节计算方法结合材料力学纯弯曲挠度公式可以得到位移为2.43 mm,这与有限元计算结果误差为4.3%。误差在可接受范围内,因此简化模型及计算方法是可信的。

在飞机初步设计阶段,对于机身开口区域可以通过强度计算得到机身开口区各部件基础尺寸。根据飞机设计相关要求^[11-12]：

(1)在纯气密载荷工况下,蒙皮环向拉应力$\sigma_t$小于控制拉伸应力$[\sigma]$

式中,$P$为气密极限载荷。式(9)可以确定蒙皮初步基础厚度$\delta_{\rm mp}$。

(2)对于未开口区蒙皮在35%极限载荷下不发生压缩弹性失稳

式中,$\sigma_{\rm cr}$为压缩载荷作用下的临界失稳应力;$\sigma$为机身开口区蒙皮最大压应力;$K_\text{e}$为压缩临界应力系数(由长桁间距$S_{\rm ch}$与框间距$S_{\rm gk}$比值决定,查飞机设计手册可得);$E$为材料弹性模量;$\mu $为泊松比;$M_{\max} $ 为最大垂向弯曲载荷;$I_0 $为未开口区截面弯曲刚度。

当$\gamma $为0$^\circ$,$\beta $为90$^\circ$时,此时简化模型即为未开口模型,同时未开口区域不需加强桁梁,即$A_{\rm jq}$为0。根据式(6)$\sim$式(8)可得

根据式(10)$\sim $式(13)可得

对于初步设计阶段,根据以往飞机统计数据可以初步确定机身框间距$S_{\rm gk}$及长桁间距$S_{\rm ch}$,根据式 (14)确定最小蒙皮折算厚度$\delta_0$。

为避免在弯曲载荷作用下机身发生总体失稳,框必须具有足够的弯曲刚度。对机身框刚度的设计要求为

式中,$I_1$为隔框惯性矩。在飞机设计初步阶段可以假定隔框横截面为正方形,由隔框惯性矩就可以得到隔框横截面面积$F_{\rm gk}$。

最后,由求得的蒙皮初步基础厚度$\delta_{\rm mp}$,蒙皮折算厚度$\delta_0$,隔框横截面面积$F_{\rm gk} $,机身框间距$S_{\rm gk}$及长桁间距$S_{\rm ch}$,结合式(1) 可以得到长桁的横截面面积$F_{\rm ch}$。

(3)对于开口区蒙皮在35%极限载荷下不发生剪切弹性失稳

式中,$\tau_{\rm cr}$为剪切载荷作用下的临界失稳应力; $\tau$为机身开口区蒙皮剪应力;$K_{\rm s}$为剪切临界应力系数(由长桁间距$S_{\rm ch}$与框间距$S_{\rm gk}$ 比值决定,查飞机设计手册可得);$F_Z$为最大垂向剪切载荷。

根据式(16)$\sim $式(18)可得几何尺寸的约束条件

对机身开口区进行初步设计时要考虑对开口结构进行加强,同时希望开口结构补强效率最优,即要使机身开口补强后的截面弯曲刚度与截面重量比值最大,即单位面积下弯曲刚度最大,令该比值为

因此,机身开口角度及加强桁梁面积最优解即求$\varDelta $的最大值,数学模型如下。

设计变量：$\gamma$,$A_{\rm jq}$;

约束条件：几何尺寸约束即式(19);

目标函数：MAX($\varDelta$)。

通过$\varDelta$对$\gamma$及$A_{\rm jq}$分别求导得到对应的极值点

联立式(20)和式(21)即可得到机身开口角度及加强桁梁面积最优解。

以某型号民用飞机为例,对于初步设计阶段可得机身初步尺寸：(1)机身典型段半径$R$ 为1430 mm;(2)机身框间距$S_{\rm gk}$取为500 mm,长桁间距$S_{\rm ch}$取为150 mm;(3)舱门所在地板平面与机身截面交点与圆心夹角,铝合金弹性模量为71 000 MPa。根据气密设计要求,纯气密载荷蒙皮应力控制拉伸应力[$\sigma ]=130$ MPa,气密载荷$P$为0.084 8 MPa。在设计工况下,机身各截面最大弯矩$M_{\max}$为$- 1 458 097.11$ N$\cdot$m,最大剪切载荷$F_Z$为$-233 642$ N。

由式(9)可得蒙皮初步基础厚度$\delta_{\rm mp}$最小为0.93 mm,取整为1 mm;由式(14)可得蒙皮折算厚度$\delta_0 $为1.89 mm;由式(15)可得隔框面积$F_{\rm gk}$最小为144.9 mm$^{2}$,取整为145 mm$^{2}$;最后根据式(1)可得长桁面积$F_{\text{ch}}$为90 mm$^{2}$。

根据式(20)和式(21)以及以上开口区基本尺寸,联立求解可得$\gamma= 45^\circ$,$A_{\rm jq} = 1081.08$ mm$^2$。此时单位面积弯曲刚度最大。经过以上计算,开口区加强桁梁面积最优解为1081.08 mm$^{2}$, 开口区开口角度最优解$\alpha =\dfrac{1}{2}\pi - \beta + \gamma = 90^{\circ} - 57^{\circ} + 45^{\circ} = 78^{\circ}$。

本文介绍了机身开口区结构刚度和强度要求,对机身开口区进行刚度分析研究以及强度分析计算,对飞机初步设计阶段机身开口区相关结构基础尺寸和开口区最优角度以及加强结构尺寸进行了详细计算,明确了开口结构刚度的影响因素,为结构设计提供指导及方向,为其他型号飞机结构设计提供一定参考意义。