由于结构优化一般都采用有限元方法分析结构, 所以用有限元直接表示孔最方便。首先将设计域划分为有限单元, 通过在任意位 置删除部分有限单元 可以近似表示任意数量和形状的孔。

第1种方法最直接, 就是将单元的"有"和"无"作为一个[0, 1]取值的离散优化变量。Xie等^{[24, 25]}提出的进化结构优化方法, 每次迭代删除一定比例(称为放弃比)效率较低的单元形成空洞。迭代过程中放弃比逐步改变一个量(称为进化比)。后来又发展出的双向进化结构优化方法^[26]还可以增加单元, 由于其方法简单有效而被广泛接受。

第2种采用放松的方法, 将[0, 1]取值的离散变量变为[0-1]的连续变量。Bendsoe等^[27]提出的均匀化方法在每个单元内嵌入一个矩形孔, 每个孔的长和宽以及角度作为优化设计变量。当孔充满单元时则单元为空; 反之, 当孔大小为零时保留单元。带孔单元的刚度矩阵需要数值方法计算, 其值实际是单元内部均匀化的结果, 这正是这个名称的来历。对于不同尺寸的孔需要事先计算出各种单元刚度矩阵。后来提出的多阶材料模型假设材料沿几个不同方向分布不同密度的微结构。多阶材料模型可以是二维或三维微结构, 不仅可以描述更复杂的材料, 而且避免了单元刚度矩阵的复杂计算^{[27, 28]}。

放松的方法会得到大量中间密度的灰色区域。虽然带有灰色区域的结构更容易接近理论解, 理论上可能更优, 但往往不是工程上期望的结果。为此, 通过罚中间密度的方法抑制中间密度。优化方法采用这样一种人工材料^[29]

$$E({\pmb x}) = \rho ({\pmb x})^pE_0 (1)$$

式中$\rho ({\pmb x})$是单元材料密度,${\pmb x}$表示位置, $E_{0}$和$E$是材料的弹性模量和计算时实际采用的弹性模量值, 指数$p> 1$是罚参数。罚参数的作用是在密度变小时单元刚度变小的速度更快, 使得中间密度会趋于零, 有效抑制了中间密度。这就形成了采用罚函数的各向同性实体或微结构优化方法(solid isotropic material or microstructure with penalization, SIMP)。有1个99行的小程序可以帮助大家理解这个方\linebreak 法^[30]。

隋允康提出独立连续拓扑变量及映射变换方法, 针对式(1)的关系研究了几个不同方案。针对几何尺寸、允许应力、刚度等几个不同性质的物理或几何量采用不同的独立的映射关系^{[31, 32]}。该方法可以用于连续体和刚架结构的优化。

水平集方法 定义一个称为水平集函数的标量函数$\varPhi({\pmb x})$。结构拓扑用这个函数表示

$$\varPhi ({\pmb x})\left\{ \begin{array}{ll} { \geqslant 0}\, ,\ \ & \hbox{实体}\\ { = 0}\, , & \hbox{边界}\\ { < 0} \, , & \hbox{空} \end{array} \right. (2)$$

式中${\pmb x}$表示优化设计变量。通过改变这个函数来改变域的内外边界实现结构拓扑优化^{[33, 34]}。产生新孔是水平集方法的一个比较困难的问题。泡泡法 通过一个特征函数决定在适当的位置结构中插入孔^[35]。几何描述方法中改变边界的能力是十分重要的性能。

Guo等^[36]和Zhang等^[37]提出可移动变形组件或孔洞法。他们事先在设计域内布置几个弹性组件或孔洞, 通过优化弹性组件或孔洞的形状和尺寸实现结构拓扑优化。相对基于单元描述或基于结点的描述方法显著减少了设计变量, 提高了优化效率, 减少了后处理工作。

Bendsoe 等^[38]提出的自由材料优化方法 将材料的弹性张量的所有分量都作为优化设计变量, 通过优化弹性张量的分布场函数实现结构拓扑优化。这种材料具有最大的优化空间, 但与真实材料不对应, 难以实现, 一般需要进一步的后处理^{[39, 40, 41, 42, 43]}。

从第1章介绍可知, 理论上, 拓扑优化结构是非均匀各向异性类桁架连续体, 而本章前2节数值优化方法旨在得到工程上经常需要的均匀各向同性带孔连续体, 这实际上是在最优解附近寻找近优解。这类方法试图将理论上最优和工程上适用两个相互矛盾的目标放在一起考虑, 引起一系列困难：为了得到等厚板限制了中间密度, 限制中间密度又导致了单元铰接, 为此又要控制梯度或周长等。解决这些矛盾的另一个思路是将这两个相互矛盾的目标放在两个独立的过程中实现：先实现理论上的最优, 再根据工程上的需要离散化, 这就是基于类桁架材料模型的优化方法^{[44, 45, 46]}。

基于类桁架材料模型的优化方法根据拓扑优化的类桁架性质建立一种类桁架材料模型。采用有限元分析方法和数学规划方法可以得到十分接近理论解的拓扑优化类桁架结构, 这种类桁架材料结构与杆件具有明确的对应关系。可以保留部分离散杆件成为桁架结构^[46]; 也可以取舍部分区域的连续分布杆件成为带孔连续体。这个过程称为离散化过程。

在应力约束优化问题中, 当拉、压允许应力不相等时, 可能会出现奇异性问题。因为当杆件截面趋近于零时, 计算应力并 不趋近于零, 存在所谓极限应力, 表现为可行域中的各部分的维度不一致, 数学优化过程的强非线性、非凸性。这些问题使得寻找全局最优解变得非常困难。

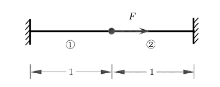
为了便于理解, 这里举一个非常简单的例子, 如图2所示一个两端固定的杆件, 中间受到一个轴向集中力。为了简单起见, 假设杆长为2, 拉、压允许应力分别为1和2, 集中力的大小为1。两段杆件的横截面积分别计作$x_{1}$和$x_{2}$, 可行域由$D_1 = \{(0, x_2 )\vert x_2 \geqslant 1 / 2\}$和$D_2 = \{(x_1 , x_2)\vert x_1 + x_2 \geqslant1\}$共同构成。前者$D_{1}$是1维空间, 后者$D_{2}$是2维空间。优化点(0, 1/2)在1维空间的端点, 远离$D_{2}$空间。如果初始点选在$D_{2}$, 则常规的数值迭代方法很难通过$D_{1}$达到优化点。

图2

	Figure Option ViewDownloadNew Window
	图2 异性问题

Cheng等^{[47, 48, 49, 50]}将常用的应力约束改写成内力约束形式, 并做适当放松, 使退化的可行子空间被扩充, 问题得到很大程度的解决, 取得重要进展。奇异性问题不仅存在于桁架, 也存在于连续体; 不仅存在于应力约束, 也存在稳定等约束问题^[51]。

但是, 一般地, 单工况下允许应力为常数时不存在奇异性问题。

许多结构拓扑优化方法研究柔度(外力功)最小化问题。这种优化问题的约束条件只有一个, 而且对局部参数不敏感, 称为全局约束条件。但是, 像强度这样最普遍的应力约束条件, 要求结构在所有位置都满足, 对局部参数敏感。离散化的数值优化方法需要满足大量的约束条件, 过多的约束条件会增加优化求解的难度。为了减少约束条件, 可以将这些大量局部约束写成一个全局整体约束形式^{[51, 52]}

$$G_{ks} = \dfrac{1}{p}\ln \sum_i {\rm e}^{pR_i } \leqslant \sigma _{ s} (3)$$

或

$$G_{kk} =\Big [\dfrac{1}{p}\sum_i (R_i )^p \Big ]^{1 / p} \leqslant \sigma _{ s} (4)$$

式中

$$R_i = \dfrac{f_i (\sigma )}{f_{\max } (\sigma )}\, f_{\max } (\sigma ) = \mathop {\max }\limits_i f_i (\sigma ) (5)$$

$f_i (\sigma )$是$i$点等效应力, $\sigma _{ s}$是允许应力, $p$是1个较大的数, 累加号表示对所有约束位置累加。较大的$p$可以增加最大应力的权重, 减少局部应力超限的机会, 但也会更容易引起迭代震荡。

以SIMP为代表的拓扑优化方法为了得到清晰的(0-1)结构, 避免大面积的灰色区域使用式(1)的罚函数方法抑制中间密度, 抑制中间密度导致棋盘格、单元铰接以及局部极小值等数值不稳定问题。

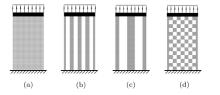
为了帮助理解这个问题, 讨论图3(a)所示矩形域(假设无限宽, 忽略边界影响)受均布力作用。假设设计域内允许应力为1, 均布外力集度为0.5, 上边为刚性不可设计域。应力约束优化结构是厚度为0.5的板。但是, 限制厚度为0或1时, 如果如图3(b)和图3(c)所示只有一半材料是同样的优化结构, 优化结果不唯一。实际优化计算中具体得到哪一个结构很大程度上取决于有限单元数量。Cheng等^[53]最早在研究加肋板优化问题时发现了这种单元网格依赖性问题。

图3

	Figure Option ViewDownloadNew Window
	图3 棋盘格现象

如果采用4结点矩形单元, 由于位移模式的双线性假设, 图3(d)的结构也 同样最优, 这就是著名的棋盘格现象。同理, 图1(b)的连续均匀径向分布杆在抑制中间密度的情况下也会出现图3(b)和图3(c)的单元依赖性和图3(d)的棋盘格现象。提高有限元的精度可以减轻棋盘格现象, 但是, 在优化后期一些区域单元数量逐渐减少。由于铰接区域的单元数过少导致计算误差过大, 需要借助周长控制、局部梯度控制、过滤等其他方法^{[54, 55]}。

工程结构实际工作环境经常具有大量不确定性。在确定条件下的最优结构在不确定性环境下可能就不再是最优了, 因此结构拓扑优化有必要考虑这些不确定性因素。不确定性因素可以与结构有关或无关, 前者的分析难度更大。可以采用鲁棒性设计优化和基于可靠性的设计优化^{[56, 57]}, 可以基于概率的和非概率的方法^[58]。

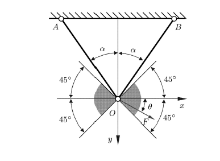
考虑不确定性的优化方法远比确定性优化方法困难, 而且优化结果也不一样。如图4所示, 集中力作用点$O$点距上边固定边距离给定的情况下, 如果确定载荷的方向在$ - 45^\circ \leqslant \theta \leqslant 45^\circ$灰色区域内, 优化结构的杆件与竖直方向的夹角$\alpha = 45^\circ $; 如果是在同样范围内的不确定载荷, 则$\alpha =35.3^\circ $^[59]。这是由于在不确定载荷下, 确定的结构需要在所有不确定载荷下都安全; 而确定性载荷下的结构只需满足一个确定载荷条件。因此, 不能用确定性载荷下的拓扑优化结果直接评判不确定载荷的拓扑优化结果。

图4

	Figure Option ViewDownloadNew Window
	图4 二杆结构

结构拓扑优化方法不仅可以实现结构优化, 还可以进行材料微结构优化形成轻质高强材料。为了能够进一步提高结构整体性能, 同时实现宏观结构和材料微结构的多尺度优化则是一个具有吸引力的研究方向。当然, 这种优化需要两个层次的嵌套, 运算量巨大, 可制造性也是一个问题。采用周期性微结构可以增加实用性、降低计算成本^[60]。微结构的材料还在散热性能方面表现出一些优良性能^[61]。

应用最早的是满应力准则的应力比公式

$$\rho _i^{k + 1} = \rho _i^k \sigma _i^k / \sigma _{ s} (6)$$

式中$\sigma _i^k $是工作应力, $\rho _i^k$是作为优化设计变量的材料参数, 上角标是迭代指标, 下角标表示位置。满应力准则用于应力约束优化问题具有很高的计算效率, 对优化设计变量不敏感, 特别适合大规模拓扑优化问题。在单工况应力约束下体积最小结构符合满应力准则, 他同时也是体积约束柔度最小结构。静定结构甚至可以一次迭代达到最优解。对于多工况或多约束的超静定结构, 拓扑优化结构并不满足满应力准则。通过构造拉格朗日函数利用极值条件也可以导出一些特定问题的优化准则, 用于结构拓扑优化分析。

优化问题的目标函数和约束函数如果都是线性函数, 则属于线性规划问题, 可以采用成熟的单纯形法求解, 通过有限次迭代得到最优解。对于非线性规划问题, 可以利用泰勒级数将目标函数和约束函数在当前点近似展开成线性规划或二次规划子问题, 用序列线性规划或序列二次规划 求解。如果将函数展开为变量的倒数形式可以改善计算性能^[62]。

Fleury^[63]和Zhang等^[64]将目标函数和约束函数用凸线性化方法展开。Svanberg^[65]提出移动渐近线方法, 移动渐近线方法后来发展出了广义移动渐近线方法, 基于梯度移动渐近线方法 和全局收敛移动渐近线方法 等多个版本$^{[66]}$。这些方法的展开式保证了优化子问题的凸性, 有较好的收敛性, 目前在结构优化领域取得良好的效果。

系列序列规划方法以及一些准则法都需要计算目标函数和约束函数的导数(敏度)。基于敏度的方法一般具有较快的收敛速度和较高的优化效率, 适合较大规模的结构拓扑优化, 特别是利用二阶导数会进一步提高优化收敛速度。但是, 导数计算本身的计算量往往很大, 特别是二阶导数计算量更大。因此, 一般只使用1阶导数, 或再加上2阶导数海森矩阵的对角元。

敏度分析有3个基本方法^[67]：虚载荷法, 状态空间法和设计空间法, 他们针对的表达式不尽相同。优化问题本身如果是非凸问题, 基于导数的方法有可能会陷入局部最优解。

遗传算法 借鉴遗传学的研究成果, 基于概率的搜索方法, 通过复制、交叉和变异几种操作逐步寻找优化点^{[68, 69, 70, 71]}。 模拟退化算法^[72]等都是属于启发式算法, 这些方法都不需要导数信息。虽然在理论上, 这些方法经过无限次地迭代就可以接近1的概率找到全局最优解, 但实际运算时也可能出现"早熟"等问题, 并不一定收敛到最优解。而且这些算法的收敛速度都很慢, 计算效率不高, 不适于大规模的寻优, 不推荐直接用于拓扑优化问题的求解。