动力源柔性牵引工作部件方式广为使用.悬挂的撞木摆动可减轻地面不平对冲车的影响,周期性地施加载荷可使摆幅增大, 得到较高撞击速度.大锤软柄的弹性变形延缓锤头加速、降低瞬间出力,而变形恢复又可使锤头进一步加速,且能减缓作用于手的反震力.扁担振动可使挑担者在肩部承载较小时迈步向前. 操作节奏是实现柔性牵引优良性能的关键.
柔性牵引是动力源与工作部件间的传动形式, 可以产生变形或运动, 起到减缓或增强工作部件的作用.攻城用冲撞车、软柄大锤以及扁担和连枷都使用了柔性牵引, 其优良特性的实现与操作节奏存在特定的关系; 相关内容或许可为振动力学 的教学[1]提供参考.
战争是检验一国实力最为直接的方法, 各国都努力发展与战争相关的技术和产业, 古往今来, 盖莫能外.城墙是防守的坚固依托[2], 《三国演义》97回详细叙述了诸葛亮多种攻城举措及遭受的挫折, 相关内容见于《三国志· 魏书· 明帝纪》, 魏国陈仓守将"昭又以绳连石磨压其冲车, 冲车折". 正如《孙子》所说 "其下攻城. 攻城之法, 为不得已".
冲车, 又称撞车, 是先秦时期出现的一种攻城器械, 《诗经· 大雅· 皇矣》、《墨子备城门》均有记载, 汉景帝刘启(公元前187– 前141)阳陵出土有撞木前端的棱锤形钢铁撞头皇矣》、《墨子备城门》均有记载, 汉景帝刘启(公元前187– 前141)阳陵出土有撞木前端的棱锤形钢铁撞头[3], 江苏连云港出土的汉简记载有西汉成帝永始四年(公元前13年)郡级武器库藏, 其中列有冲车37辆及相关备件的名称和数量[4].
古代冲车的具体形式似已难考, 最初可能将粗木直接架在车轴上或者固定在车体上, 结构相对简单; 不过, 冲撞反力将使撞木偏离车轴或损伤车体, 影响持续撞击.实际使用者一定会发现, 将撞木悬挂起来操作更为便利, 撞击力度也能增强.或许, "飞冲"就是悬挂撞木的冲车, 不必理解为投射器[3].国内多个影视城复制有图1所示的冲车, 士兵可在内部推车而行, 以防护城楼投下的石块或发射的箭矢.
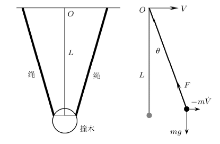
撞木相对于车体平动, 各处运动特征相同, 可以摆长LL、质量为mm的单摆作为力学模型(图2), 其在悬挂点OO被质量为MM的车体 牵引向前, 牵引速度为V.
记摆绳内力为FF, 摆角为θ , 满足
式中, $\dot\theta$为角速度, $\ddot\theta$为角加速度, $\dot V$为加速度.
$mL\ddot\theta = - mg\sin \theta - m\dot V \cos \theta \quad (1)$
$mL(\dot\theta )^2 = F - mg\cos \theta + m\dot V \sin\theta \quad (2)$
为简单起见, 将平整路面推行时冲车所受阻力折算到车轴上, 其与竖直方向的载荷NN 成比例, 比例系数为 $\mu; 士兵的推力为; 士兵的推力为R$, 满足
$M\dot V = R + F\sin \theta - \mu N \quad (3)$
$N = F\cos \theta + Mg \quad (4)$
匀速推行时 $\theta =0$, 推力$R$用于克服阻力 $\mu (M+m)g$. 若遇到路面凸起而阻力增加, 则车速减小; 由式(1)可知撞木相对于车 向前运动, 即 $\theta > 0$.在最远点附近角速度较低, 由式(2)和式(4)可知$F$和$N$减小, 阻力也将随之减少; 此外, 从式(3)可以看到, 拉力$F$的水平分力有助于车体速度的恢复.当然, 撞木通过中心点向后摆动时将阻碍车体向前, 但冲车应已通过凸起而向下运动, 即悬挂撞木具有抹平扰动的功效.
设车速$V =1$m/s 即 3.6km/h, 摆长$L=1$m; 若车因阻碍突然停止, 则撞木可升高5.1cm, 最大摆角 $\beta =18.4^{\circ}$, 绳中拉力达到$mg \cos \beta $, 引起车体对地面的竖直压力减少了$0.099mg$, 并对车体产生水平拉力$0.299mg$. 后者数值较大, 能够产生显著效果.此外, 摆动周期为2.0s, 推车者也有足够时间作出反应. 这些计算结果在定性上是可信的.
冲车若停在泥土地面时间稍长, 车轮就会因土体蠕变而陷入, 加之轮轴等处静摩擦总是大于动摩擦, 因而推车初始阻力较大.若启动困难, 也可先推动撞木摆动, 在其接近前方最高点时推车向前.
与荡秋千类似$^{[5]}$, 周期性地施加载荷引起共振, 可以使撞木摆动的幅度逐步增大, 所获得的速度总能大于士兵步行的推车速度.通过战前训练, 确定撞木所能达到的最大振幅, 在其从后方最高点向前摆动时推车向前, 在最低点或稍过最低点发生撞击; 如此操作, 则撞击速度是摆动速度与推车速度之和, 肯定优于撞木与车固定而整体撞击的效果.
锤是敲打的用具, 大小悬殊, 种类繁多. 此处单说大锤, 供石工击钎打孔 (图3)和铁匠锻打熟铁, 近来也用于混凝土的拆除.锤柄可用两三条竹片拼贴而成, 但多是弹性很好的白蜡杆.
软柄不震手且省力, 这是使用者的经验之谈. 不过, 因出力与速度并不合拍, 软柄大锤的挥甩也有顺逆之分, 需得把握好节奏, 正如 弹性 扁担挑运者只有熟悉扁担振动节奏之后才能轻快前行[6]."十八磅的软柄大锤, 非力大如牛的铁匠高手难以操控啊, 可在少年的手里竟是那般轻松自如, 仿佛是他身体的外延", 《生死疲劳》中这句话想来是莫言亲见之后的赞叹.
为理解软柄大锤的工作原理, 建立图4所示的简化模型, 即假设手柄为悬臂梁, 刚度为KK,
牵引质量为mm的锤头加速运动, 撞击固定物体.
设牵引速度为$V$, 锤头位移为$u$, 则有
在时间$t =0$时 $u=0$, $u_{t}=0$.
$m\dfrac{d^2u}{d t^2} = K(Vt - u) \quad(5)$
若速度$V$恒定, 解得锤头位移和速度
$u = V(\omega t - \sin \omega t) / \omega \quad (6)$
$u_t = V(1 - \cos \omega t) \quad (7)$
以及牵引力
$ F = K(Vt - u) = (KV\sin \omega t) / \omega = V\sqrt {Km} \sin \omega t \quad(8)$
式中频率
$\omega = \sqrt {K / m} \quad(9) $
若撞击时间恰巧在$T = \pi / \omega $, 速度达到最大值$2V$, 即弹簧使撞击能量提高4倍; 而撞击时牵引力为零、弹簧恢复原状, 即处于松弛状态, 人手所受撞击载荷的影响较小.牵引力的最大值与$K$ 相关; 减小刚度$K $可减小出力, 但延长加速时间和行程.
参数$T$ 即自由振动的半周期可作为大锤的特征时间. 此外, 速度在峰值附近变化较缓, 由式(7) 可知, 在 (0.86 $\sim $1.14)$T$ 之间即在近30%的范围内, 锤头撞击速度都大于 1.90$V$.只要锤头质量与软柄尺度协调, 完全可以将软柄的弹性变形能用于撞击.
白蜡树, 别名青榔木、白荆树, 繁殖便利、生长快速, 河南宁陵等地有规模种植, 因其树杆具有极好的韧性而得到广泛使用[7]. 下面笔者对所购白蜡杆及8磅大锤的力学特征略作说明.
锤柄悬臂长1m时, 3.6kg锤头下沉11cm, 刚度$ K =320$N/m, 计算频率为9.4s$^{-1}$, 与自由振动周期0.6s大致相符, 相应的 动刚度$ K_{\rm d} =395$N/m, 动态杨氏模量$E_{\rm d} =3.3$GPa.直径30mm、长1m的白蜡杆质量约0.6kg, 影响较小, 没有参与计算.
不过, 截取长53mm 、直径约31mm的杆头, 单轴压缩的杨氏模量为 1.5GPa (硬质木材可达10GPa), 计算的悬臂梁刚度仅为 180N/m, 与实测值差别较大.这可能源于试样几何尺寸不规范以及纤维压缩模量低于拉伸模量. 下面以实测振动周期0.6s及动态模量3.3GPa为基准进行说明.
长 1m、直径3cm的白蜡杆竖直向下驱动锤头水平匀速运动, 锤头重 3.2kg, 在最佳时间0.3s时撞击速度可以达到牵引速度的两倍; 若是18磅大锤, 则最佳时间为 0.45s. 当然, 实际牵引并不是匀速状态, 最初也有加速过程, 而弹簧变形延缓锤头加速、降低瞬间出力, 使牵引速度易于增加; 牵引速度恒定值$V$, 锤头在达到该速 度之前弹簧伸长储存能量, 其后, 弹簧恢复状态释放能量使锤头进一步加速.
由于锤头很重而锤柄较轻, 依打击中心[8] 所确定的锤柄长度较短, 并不适用于大锤; 而白蜡杆的韧性能够消除冲击载荷.
如果敲砸地面, 锤柄也就较长, 抡锤者通常都是双手分开握柄, 往复地高举低砸; 若空间许可, 抡锤者多侧身转体从身后举起大锤.上举初期锤柄的弹性变形可以延缓锤头升高和速度增加, 减小出力而避免腰部肌肉劳损(图5); 而接近最高点时势能不再增加, 挥臂速度降低, 锤头惯性可使软柄向人体背后弯曲, 储蓄动能; 人只要手握锤柄竖直向上, 软柄弯曲、锤头重力势能降低转换为弹性势能, 如图3所示.
人挥柄向前、向下运动, 锤头重力势能以及锤柄弹性势能将转换为锤头的动能. 锤头撞击钢钎的反冲力使锤头升高以及锤柄变形, 减少了手掌 震动, 而锤柄变形也有利于手臂运动的换向. 另一方面, 假如锤柄完全刚性, 则上挥初期速度受到制约, 人容易用力过猛而受伤; 人举起大锤之后若不能准确控制减速过程, 不仅浪费能量, 而且会站立不稳.
若空间狭小, 打钎锤铁时大锤只能往复地高举低砸; 不过, 只要空间许可, 大锤都是圆抡:双手相并抓住锤柄尾端, 侧身将大锤由下方向后甩起, 上举过头顶, 再转身挥臂下砸; 借着锤头的回弹而转身, 再加速下摆大锤以积蓄能量而上举.软柄的弹性变形可以协调手臂的挥舞与锤头的运动, 连绵不断地抡砸固定位置的钎头.
"红旗渠的故事"22分钟处有如此抡锤砸钎的视频[9].此时锤柄通常较短, 约为65cm, 而悬臂梁刚度与臂长3次方相关, 依前 述数据, 则白蜡杆刚度增大为1438N/m; 若大锤为18磅即8kg, 则有 $\omega =13.4$s$^{-1}$, 特征时间为$T = 0.23$s.
抡锤头从最高点砸到钢钎的距离约为 2m, 该距离自由落体的时间为0.63s; 实际砸锤时间因人而异, 估计在0.3s以内, 与大锤特征时间$T$相符.当然, 抡锤者会依据自身力量调整握手位置, 以改变锤柄长度使之"顺手"; 另一方面, 抡锤初期都是逐步提速以确认最佳速度——省力而不震手.
冲车柔性牵引撞木, 因其可以自由摆动而减轻地面不平对推车的影响, 类似于减振; 周期性地施加载荷使撞木摆幅增大可得到更高撞击速度. 若没有冲车则可用扁担、绳索合抬圆木撞击.调整步伐节奏, 则撞击速度达到士兵行走速度和绳索摆动速度之和, 效果优于肩扛, 且能避免 反冲力对士兵的伤害.
工具手柄的材质及连接方式因用途和地域而各不相同.白蜡杆因几何尺寸和变形特性恰好适用于大锤, 柔顺地协调手臂与锤头的运动 过程, 积蓄力量而用于一刹------砸铁破石.上天造物, 刚柔并济, 真是尽善尽美啊.不过, 破土农具如镢头、钉耙和铁塔, 都是用刚度较高的硬木或竹杆作柄[10].土体硬度不同, 破土时间不等, 前述手柄的弹性变形似不易应用; 而破土过程使手柄速度逐步降低, 也就不会产生显著的反震而伤手.此外, 破土用具关键是刃口, 重量相对较轻而不存在上举的困难, 也就不必选用软柄.
扁担挑运综合运用了上述两种形式的柔性牵引.人走动时双脚轮替着地而具有速度脉动, 荷物因绳索的相应摆动在水平方向近乎匀速向前, 减少了人体所作的无用功; 而绳索使扁担作用力周期变化引起扁担共振而得到放大, 可使挑担者在肩部承载较小时迈步向前.扁担形状近似于等强度的悬臂梁, 降低了刚度, 使扁担振动频率与走动步伐协调.不过, 若担物行走于坡路、台阶或陡峭的山路, 为了避免不规则的振动, 需要缩短绳索的长度、增加扁担的刚性乃至放弃肩挑而选用背驮的方式运物[6].
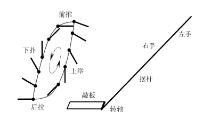
连枷的转轴亦可看作柔性牵引.手握摆杆周期性后拉、上举、前推和下扑, 即可使敲板作圆周运动而进行农作物的脱粒(图6).通常经人指点再略作练习, 即可获得节奏感而有韵律地劳作, 确保转轴端同时或略后于敲板前端到达地面[11, 12].
若将敲板横转而固定于摆杆端部即类似于翻耙, 则结构简单, 操作也更为便利.也许连枷的原始结构就是如此; 不过, 在上举和下扑转换时需略作停顿而不能连续作业, 降低击打频率, 人也易于疲劳; 其敲板击打谷物的速度等同于摆杆端点的速度.真实连枷转轴的柔性牵引使敲板连续运动, 其击打是自身旋转速度与摆杆端点牵引速度之和, 前者在最高点并不为零, 且下扑过程仍会增加(图6), 效率也就更高.
柔性牵引设计还具有其他形式和优点, 如马车挽具的多层系杆可以将车体所受阻力均衡地分配给各匹驾马[13], 机械的皮带传动通过打滑以限制最大载荷而保护动力源, 等等.
柔性牵引是动力源与执行构件之间的一种传动形式, 其连接部件通常具有较复杂的结构, 可以抹平扰动, 也可以将载荷、速度等力学量在特定时段内集中.先民在生活实践中逐步掌握了相关技艺, 并优化了结构参数.当然, 动力源与工作部件的运动并不能完全同步, 需要依照一定的节奏操作才能获得效果; 而节奏的掌控是练习的结果.
致谢 衷心感谢苏承东高工关于软柄大锤的有益讨论.
The authors have declared that no competing interests exist.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|