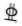
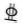
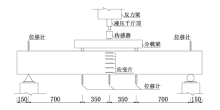
单筋矩形截面梁横截面宽200 mm, 高300 mm, 梁长2 400 mm, 净跨2 100 mm, 受拉筋和架立筋分别采用3根 12和 2根 8的HRB400钢筋, 箍筋采用Φ 6的HPB300钢筋, 间距100 mm, 纯弯段不设箍筋, 混凝土标号C40, 保护层厚度25 mm. 梁的尺寸及配筋形式如图1所示. 在材料力学单向拉伸或压缩章节中, 可以通过试验测上述钢筋的拉伸及混凝土的拉伸和压缩性能, 得到建立力学模型所需的参数.

图1

	Figure Option ViewDownloadNew Window
	图1 梁的尺寸及配筋示意图

为了让同学们理解纯弯梁在加载过程中受弯开裂的现象, 试验采用三分点加载, 加载设备为分离式油压千斤顶(型号：QF50T), 采用单调分级加载机制, 在混凝土开裂前每级以5 kN缓慢加载, 持荷10 ~15 min. 若梁在加载过程中开裂, 取前一级载荷值为开裂载荷实测值; 当在规定的持荷时间内出现裂缝时, 取本级载荷与前一级载荷的平均值作为开裂载荷实测值; 当在规定的持荷时间结束后出现裂缝时, 取本级载荷值作为其开裂载荷实测值. 加载形式及装置、现场加载试验情况如图2和图3所示.

图2

	Figure Option ViewDownloadNew Window
	图2 试验装置及位移测点布置图

图3

	Figure Option ViewDownloadNew Window
	图3 现场加载试验图

为了让同学们理解平截面假定, 试验测量数据主要为跨中混凝土梁截面沿高度方向的应变. 载荷、应变等数据使用TDS-530系统(日本东京测器研究所生产)采集. 加载过程中采用放大镜持续观测裂缝的出现, 并记录对应的载荷值.

通过试验得到钢筋混凝土梁的开裂载荷为37.5 kN, 开裂前后钢筋混凝土梁跨中截面沿高度方向的混凝土应变的分布如图4所示.

图4

	Figure Option ViewDownloadNew Window
	图4 梁跨中沿截面沿高度方向的应变分布

由图4可知, 梁跨中横截面沿高度方向的应变基本符合平截面假定, 混凝土开裂后虽然梁下部的应变增幅加大, 但也可以近似认为其应变符合平截面假定. 通过该试验结果分析, 同学们对梁弯曲时的平截面假定的理解会更加深入.

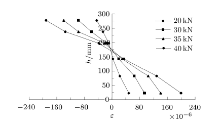
(1)根据图4的试验结果, 钢筋混凝土梁在开裂前后的应变基本符合平截面假定, 因此在计算时可以认为钢筋混凝土梁在刚发生开 裂时符合平截面假定.

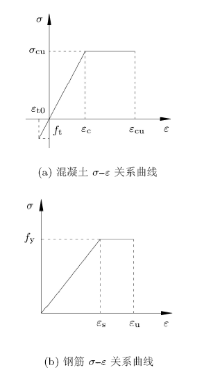
(2)根据文献[5], 在达到最大拉应力之前混凝土的应力--应变关系曲线几乎呈直线上升, 在最大拉应力之后, 曲线急剧下降; 根据 文献[6], 当 加载到曲线最高点时, 混凝土已经发生开裂, 因此计算时不考虑下降段, 即认为受拉区边缘的工作应力达到混凝土 抗拉强度时发生开裂. 在混凝土开裂时梁受压区应力较小, 应力--应变关系处于弹性阶段. 建立力学模型时混凝土的应力--应变关系以图5(a)表示.

图5

	Figure Option ViewDownloadNew Window
	图5 材料 σ-- ε关系曲线

(3)钢筋的应力--应变曲线采用两段式, 如图5(b)所示, 梁受拉区混凝土开裂时钢筋处于线弹性阶段.

在提出基本假设时, 同学们可以根据自己的试验结果, 也可以基于已有的研究成果, 这样不仅可以培养学生的试验分析能力, 也 可以提高学生查阅相关专业文献, 利用已有成果解决工程问题的能力.

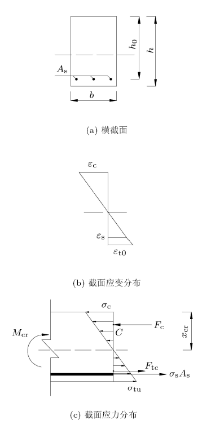
在纯弯段, 梁横截面上沿竖直方向上的应力分布为下部受拉上部受压, 在边缘处拉、压应力分别达到最大, 且处于单向应力状 态. 由于混凝土材料的抗拉强度远小于抗压强度, 因此梁的强度条件为当梁受拉区边缘的最大工作应力 σtu达到混凝土抗拉强度 ft时, 梁下边缘发生开裂. 截面的计算简图如图6所示.

图6

	Figure Option ViewDownloadNew Window
	图6 梁即将开裂时的计算简图

在根据图6(b)得, 几何关系如下

$\dfrac{1}{\rho _{\rm cr} } = \dfrac{\varepsilon _{\rm t0} }{h - x_{\rm cr} } = \dfrac{\varepsilon _{\rm c} }{x_{\rm cr} } = \dfrac{\varepsilon _{\rm s} }{h_0 - x_{\rm cr} } \quad(1) $

式中, ρcr为混凝土梁刚要发生开裂时的曲率半径; εt0为混凝土达到抗拉强度 ft时对应的应变; εc为混凝土梁刚要发生开裂时梁上边缘压应力 σc对应的应变; εs为钢筋拉应力 σs对应的应变; xcr为梁刚出现弯曲裂纹时的受压区高度; h为梁截面高度; h0为截面的有效高度.

梁受拉区混凝土即将开裂时, 受压区混凝土的应力较小, 可认为压应力沿横截面呈线性分布, 根据图5(a)所示的混凝土的应力--应变关系以及图6(b)受拉区混凝土的应变分布, 可近似认为在受拉区混凝土在即将开裂时的拉应力也呈线性分布, 如图6(c)所示, 此时钢筋处于线弹性阶段, 根据胡克定律, 得出如下物理关系

σc=Ecεc, ft=σtu=Ecεt0, σs=Esεs(2)

式中, Ec和 Es分别为混凝土和钢筋的模量. 当梁受拉区边缘的最大工作应力 σtu=ft时, 沿梁轴向建立静力平衡方程： ∑‍Fx=0, 得

$\dfrac{1}{2}f_{\rm t} b(h - x_{\rm cr} ) + \sigma _{\rm s} A_{\rm s} - \dfrac{1}{2}\sigma _{\rm c} x_{\rm cr} b = 0 \quad(3) $

近似认为 εt0=εs, 并代入式(2)后, 再代入式(3), 整理后得

$x_{\rm cr} = \dfrac{A + 2\alpha _1 A_{\rm s} }{A + \alpha _1 A_{\rm s} } \cdot \dfrac{1}{2}h \quad(4) $

式中, A=bh为梁横截面面积; As为受拉钢筋的横截面面积; α1为系数, 其值为 α1=EsEc; 将上述参数代入式(4), 即可求得受压区高度 xcr.

取梁受压区作用点 C建立力矩平衡方程： ∑‍MC=0, 得

$ M_{\rm cr} - \dfrac{1}{2}f_{\rm t} b(h - x_{\rm cr} )\Big[\dfrac{2}{3}(h - x_{\rm cr} ) + \dfrac{2}{3}x_{\rm cr} \Big ] - \\ \qquad \sigma _{\rm s} A_{\rm s} \Big (h_0 - \dfrac{1}{3}x_{\rm cr} \Big ) = 0 \quad(5) $

联合式(1)、式(2)和式(5)解开裂弯矩 Mcr, 得

$M_{\rm cr} = \dfrac{1}{3}f_{\rm t} A(h - x_{\rm cr} ) + \alpha _1 f_{\rm t} A_{\rm s} \Big (h_0 - \dfrac{1}{3}x_{\rm cr} \Big ) \quad(6) $

对于图2所示的三分点加载, 钢筋混凝土梁的开裂载荷 Pcr可用下式计算

$P_{\rm cr} = \dfrac{6M_{\rm cr} }{l_0 } \quad(7) $

式中 l0为梁的净跨.

虽然同学们在学习材料力学时, 还未接触水工钢筋混凝土结构, 但是该力学模型对专业知识要求不高, 材料轴向拉伸和压缩的力学试验在材料力学前面的章节中已经学过, 只需了解钢筋混凝土的基本构成即可, 通过简要讲解, 低年级本科生完全可以理解. 上述力学模型的建立过程, 尽管只是将材料力学的基本理论进行了综合运用, 但是可以让同学们体会到运用材料力学建立力学模型解决工程实际问题的一般方法.