笛沙格定理的结构力学分析再证明

引用本文

王崇安, 邢沁妍. 笛沙格定理的结构力学分析再证明. 力学与实践, 2018,40(2): 210-213 复制到剪切板

Doi: 10.6052/1000-0879-17-214
Permissions

《力学与实践》编辑部所有

笛沙格定理的结构力学分析再证明

王崇安²⁾, 邢沁妍

清华大学土木工程系,北京 100084

2) E-mail：wca14@mails.tsinghua.edu.cn

收稿日期: 2017-10-06

资助项目: 清华大学教学改革项目资助.

摘要

结构力学中的几何组成分析方法与射影几何存在深刻的内蕴关系. 这种内蕴关系可以被用于笛沙格定理的证明. 通过构造一种特殊的杆件体系,从几何组成分析与受力分析两个角度进行分析,采用“算两次思想”分别得出杆件体系几何可变分别与笛沙格定理的条件与结论等价,从而证明笛沙格定理与其逆定理.

关键词: 射影平面; 笛沙格定理; 多余约束; 几何组成

中图分类号:O342 文献标志码:A

文章图片

笛沙格定理(Desargues’ Theorem)是平面射影几何中一条著名定理, 由数学家笛沙格(Girard Desargues)于1639年提出, 是射影几何学的开端. 过去150年内, 众多力学家在射影几何的范畴研究杆系结构的几何组成. 1863年, Rankine^[1]提出了结构自由度的仿射不变性. 1982年, Wunderlich^[2]从几何组成分析的角度阐明了结构的射影不变性; 同年, Crapo等^[3]从受力分析的角度阐明了结构的射影不变性.

由于笛沙格定理深刻的对称性与几何学内涵, 迄今为止, 众多专家学者给出了许多种基于几何法或是综合法的证明^[4]. 然而, 尽管结构的几何组成和内力有着良好的射影几何性质, 却没有文献从结构力学的角度诠释笛沙格定理. 基于对力学的重要分支— — 结构力学的学习与实践, 本文开创性的从结构力学的角度对笛沙格定理进行分析再证明. 依次构造平面和空间杆件体系, 从几何组成分析与受力分析两个不同的角度, 运用铰接三角形规律^[5]与零载法^[6], 在射影几何范畴内分析该种体系的几何组成^[7], 证明了笛沙格定理的平面和空间两种情形, 揭示了结构力学和射影几何的联系.

1 拓广平面上笛沙格定理

笛沙格定理建立于射影平面的一种模型— — 拓广平面上. 在此首先给出拓广平面的定义^[8].

拓广平面可以看作由欧几里得平面和一条无穷远直线的组合. 拓广平面内的点和直线定义如下：

(1) 在每一条欧几里得平面的直线上, 添加一个无穷远点, 构成拓广平面上的直线.

(2) 相互平行的直线上的无穷远点相同, 不平行直线上的无穷远点不同.

(3) 无穷远点的集合构成无穷远直线.

拓广平面满足如下两条重要性质^[9]:

(1) 任意两点确定一条直线. 其中, 两个无穷远点确定一条无穷远直线.

(2) 任意两条直线相交于一点. 其中平行直线相交于无穷远点.

拓广平面上, 笛沙格定理及其逆定理叙述如下：

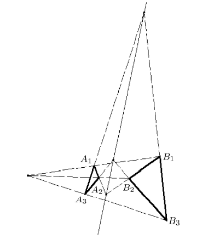
笛沙格定理(Desargue’ s theorem) 图1所示, 对于拓广平面上的两个三角形, 如果它们的3个对应顶点的连线 $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ 交于一点, 那么它们的3个对应边所在直线的交点共线.

	Figure Option View Download New Window
	图1 笛沙格定理示意图

逆定理如图1所示, 对于拓广平面上的两个三角形, 如果它们的三个对应边所在直线的交点共线, 那么它们的3个对应顶点的连线 $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ 交于一点.

2 平面杆件体系的几何组成与笛沙格定理

2.1 平面杆件体系的构造

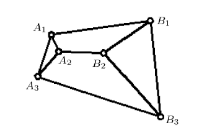
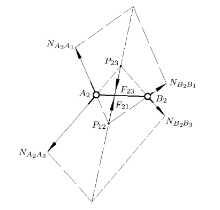
为证明笛沙格定理, 构造如图2所示的平面杆件体系. 在结构力学几何组成分析的范畴内, 该杆件体系的每一个杆件均视为刚体, 每一个铰点均视为理想铰约束. 下文对其进行几何组成分析.

	Figure Option View Download New Window
	图2 标系示例

图中共有9根链杆和6个复铰点, 其中每个铰点连接三根杆. 以图示体系链杆作为分析对象, 每根链杆有两个平动自由度与一个转动自由度, 共27个自由度数, 每个复铰连接3根链杆, 约束住4个自由度. 总约束数为24个. 如果所有约束均为有效约束, 体系仅有3个刚体自由度, 其内部即为几何不变体系. 否则, 如存在多余约束, 体系内部即为几何可变体系.

对体系杆件的内力进行受力分析可以判断是否存在多余约束, 而对体系的可变性做出几何分析可以判断体系是否为可变体系. 根据结构力学的理论, 两种分析方法得出的结果等价, 下文分别从这两个角度出发证明笛沙格定理.

2.2 杆件体系的几何分析

结构力学给出的平面几何组成分析铰接三角形规律有以下两种等价的表述形式^[5]：

如果两个刚片由3个链杆相连, 那么结构为几何可变体系, 当且仅当三链杆共点.

如果3个刚片两两铰接, 那么结构为几何可变体系, 当且仅当三铰共线. 其中, 两个刚片由两根链杆相连等效于它们由一个虚铰相连, 虚铰的位置在两根链杆的交点处.

根据结构力学理论^[5], 铰接三角形规律在拓广平面内适用. 下文将通过几何的方法分析几何组成不变的等价条件.

对图2所示的链杆体系. 利用铰接三角形规律, 将 $Δ A_{1} A_{2} A_{3}$ 和 $Δ B_{1} B_{2} B_{3}$ 视为两个刚片. 由图3所示, 两个刚片由 $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ 三根链杆连接. 由铰接三角形规律, 当且仅当 $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ 三链杆交于一点时, 图示杆系为几何可变体系.

	Figure Option View Download New Window
	图3 虚铰位置示意

将链杆 $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ 视作3个刚片. 由图3可以看出, $A_{1} B_{1}$ , $A_{2} B_{2}$ 两个刚片由链杆 $A_{1} A_{2}$ , $B_{1} B_{2}$ 相连, 因此, 它们等效于铰接在虚铰 $P_{12}$ 处. 同理 $A_{3} B_{3}$ , $A_{2} B_{2}$ 两个刚片等效于由链杆 $A_{2} A_{3}$ , $B_{2} B_{3}$ 相连, 等效于铰接在虚铰 $P_{23}$ 处; $A_{3} B_{3}$ , $A_{1} B_{1}$ 两个刚片等效于铰接在虚铰 $P_{13}$ 处. 由铰接三角形规律, 当且仅当 $P_{12}, P_{23}, P_{13}$ 三虚铰共线时, 图示杆系为几何可变体系.

以上的分析结果可以抽象成图2所示的计算自由度为零的杆件体系几何可变的两个等价条件, 如下：

(1) 杆件体系为几何可变体系等价于拓广平面内 $P_{13}, P_{23}, P_{12}$ 三点共线, 其中 $P_{13}, P_{23}, P_{12}$ 分别是 $A_{1} A_{3}$ 与 $B_{1} B_{3}$ , $A_{2} A_{3}$ 与 $B_{2} B_{3}$ , $A_{1} A_{2}$ 与 $B_{1} B_{2}$ 的交点.

(2) 杆系为几何可变体系等价于拓广平面内 $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ 三线交于一点.

综合以上两条命题, 可以推导出如下结论：

拓广平面内, $P_{12}, P_{23}, P_{13}$ 三点共线等价于 $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ 三线交于一点. 这就是笛沙格定理及其逆定理

由于在拓广平面内, 任意两点确定一条直线、任意两条直线有唯一交点. 因此, 上述证明具有一般性.

2.3 杆件体系的内力分析

根据前文分析, 如果上述杆系所有约束均为有效约束, 则体系内部即为几何不变体系. 因此, 从多余约束的角度进行分析和从几何可变性角度进行分析得出的结论一致.

根据零载法, 如果结构中不存在多余约束, 那么当结构所受外载荷为0时, 结构中所有构件的内力必然为0. 下文从受力分析的角度分析结构中存在多余约束的等价条件.

仍构造如图2所示的链杆体系.

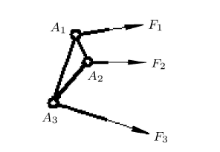
对铰接三角形 $Δ A_{1} A_{2} A_{3}$ 进行受力分析, 切断 $A_{1} B_{1}, A_{2} B_{2}, A_{3} B_{3}$ 三根链杆, 暴露出 $F_{1}, F_{2}, F_{3}$ 三个轴力. 隔离体示意图见图4.

	Figure Option View Download New Window
	图4

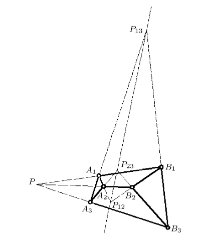
由三个铰铰接形成的三角形为静定体系, 其内部不存在多余约束. 因此整个体系存在多余约束等价于无外载荷时三个连接链杆中存在非零内力.

隔离体不受外载荷作用, 因此, 三个轴力达成平衡(如图4所示). 根据力矩平衡, 如果杆件体系的内力有非零解, 那么图3中的三个轴力的作用线 $A_{1} B_{1}, A_{2} B_{2}$ 与 $A_{3} B_{3}$ 必然相交于一点. (平行即为交于无穷远点)

如果链杆 $A_{1} B_{1}$ , 链杆 $A_{2} B_{2}$ 与链杆 $A_{3} B_{3}$ 共点, 设 $F_{2}$ 不为零, 由于三力共点, 由力的分解唯一性, 存在唯一的非零 $F_{1}, F_{3}$ . 因此, 存在非零的 $F_{1}, F_{2}, F_{3}$ 解使得杆系平衡.

综合以上两条结论可以得出：杆件体系中的内力存在非零解等价于 $A_{1} B_{1}, A_{2} B_{2}$ 与 $A_{3} B_{3}$ 交于一点.

对连接链杆进行受力分析. 将链杆 $A_{1} A_{2}$ , $A_{1} A_{3}$ , $A_{2} A_{3}$ , $B_{1} B_{2}$ , $B_{1} B_{3}$ , $B_{2} B_{3}$ 截断, 得到3个隔离体. 分别对 $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ 杆进行受力分析. 由于杆件体系的对称性, 仅需分析其中一个隔离体, 其结论可以推广到另外两个隔离体. 下面以 $A_{2} B_{2}$ 杆为例. 假设轴力存在非零解.

如图5所示, 在切断链杆后, 原有轴力暴露出来.

	Figure Option View Download New Window
	图5 隔离体取法

$A_{2}$ 端受到 $A_{1} A_{2}$ , $A_{2} A_{3}$ 的作用, 暴露出轴力 $N_{A_{2} A_{1}}, N_{A_{2} A_{3}}$ . $B_{2}$ 端受到 $B_{1} B_{2}$ , $B_{2} B_{3}$ 的作用, 暴露出轴力 $N_{B_{2} B_{1}}, N_{B_{2} B_{3}}$ . 将 $N_{A_{2} A_{1}}$ 和 $N_{B_{2} B_{1}}$ 合成为力 $F_{21}$ , 作用点为直线 $A_{1} A_{2}$ 与 $B_{1} B_{2}$ 的交点 $P_{12}$ ; 将 $N_{A_{2} A_{3}}$ 和 $N_{B_{2} B_{3}}$ 合成为力 $F_{23}$ , 作用点为直线 $A_{3} A_{2}$ 与 $B_{3} B_{2}$ 的交点 $P_{23}$ . 当且仅当 $F_{21}$ 力与 $F_{23}$ 力等大反向时, 杆的轴力存在非零解. 此时, $F_{21}$ 力与 $F_{23}$ 力的作用线均在 $P_{12} P_{23}$ 直线上.

同理可得, 如果选取 $A_{1} B_{1}$ 杆作为隔离体, 那么 $A_{1} A_{2}$ 杆和 $B_{1} B_{2}$ 杆对 $A_{1} B_{1}$ 杆的作用力 $F_{12}$ 指向 $P_{12} P_{13}$ 方向, 作用点为 $P_{12}$ .

由作用力与反作用力的关系, $A_{1} A_{2}$ 杆和 $B_{1} B_{2}$ 杆对 $A_{1} B_{1}$ 杆的作用力为 $F_{12} = - F_{21}$ , 方向也沿 $P_{12} P_{23}$ 方向.

综合以上两条结论, $P_{12} P_{13}$ 方向与 $P_{12} P_{23}$ 方向相同, 暨 $P_{12}, P_{23}, P_{13}$ 三点共线. 因此, 如果杆件体系中的内力存在非零解, 则 $P_{12}, P_{23}, P_{13}$ 三点共线.

当 $P_{12}, P_{23}, P_{13}$ 三点共线时, 非零轴力需要满足以下条件：

(1) $A_{1} A_{2}$ 杆和 $B_{1} B_{2}$ 杆轴力合力通过 $P_{12} P_{23} P_{13}$ 轴线.

(2) $A_{1} A_{3}$ 杆和 $B_{1} B_{3}$ 杆轴力合力通过 $P_{12} P_{23} P_{13}$ 轴线.

(3) $A_{2} A_{3}$ 杆和 $B_{2} B_{3}$ 杆轴力合力通过 $P_{12} P_{23} P_{13}$ 轴线.

(4) 三个轴力合力大小相等, 其中 $A_{1} A_{2}$ , $B_{1} B_{2}$ , $A_{2} A_{3}$ , $B_{2} B_{3}$ 四杆轴力正负号相同, $A_{1} A_{3}$ , $B_{1} B_{3}$ , 两轴力正负号与上述四根杆上轴力正负号相反.

任意给定一个轴力合力的大小与方向时, 根据力的分解唯一性, 满足上述4个条件的轴力均存在唯一的非平凡解. 因此, 如果 $P_{12}, P_{23}, P_{13}$ 三点共线. 杆件体系内部可以存在内力非零解.

综合以上对充分性和必要性的分析证明可以得出：结构中的内力存在非零解等价于 $P_{12}, P_{23}, P_{13}$ 三点共线.

通过选取铰接三角形作为隔离体进行受力分析, 杆系中存在非零内力等价于 $A_{1} B_{1}, A_{2} B_{2}$ 与 $A_{3} B_{3}$ 交于一点. 通过选取连接链杆作为隔离体进行受力分析, 杆系中的内力存在非零解等价于 $P_{12}, P_{23}, P_{13}$ 三点共线. 综合以上两个命题, 可以推导出如下结论：

拓广平面内, $P_{12}, P_{23}, P_{13}$ 三点共线等价于 $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ 三线交于一点.

可以看出, 内力分析和几何分析导出了相同的结论.

3 空间笛沙格定理推广

为了证明平面情形的笛沙格定理, 上文构造了平面杆件体系. 对于空间情形, 可类似的构造空间杆件体系, 以空间杆件体系的几何组成分析方法分析和证明笛沙格定理的空间情形.

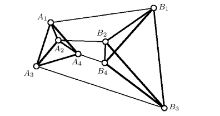
空间笛沙格定理^[10] 已知两个四点体的对应点的四条连线交于一点, 那么这两个四点体的对应棱的6个交点在一个平面上.

为了证明空间笛沙格定理, 构造由两个三棱锥和四条链杆组成的杆件体系. 杆系(图6)由两个三棱锥 $A_{1} A_{2} A_{3} A_{4}$ , $B_{1} B_{2} B_{3} B_{4}$ 组成, 其中三棱锥的节点由链杆两两相连, 使得每个三棱锥均为几何不变体系. 三棱锥间节点由4根链杆, 连接 $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ , $A_{4} B_{4}$ . 每个节点均为铰接节点.

	Figure Option View Download New Window
	图6 空间标系示意

倘若四点体的对应点的四条联线交于一点, 那么, $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ , $A_{4} B_{4}$ 4根链杆交于一点. 将4根链杆截断, 由于两个刚体由交于一点的4根链杆连接, 链杆中可以存在非零内力. 链杆系有3个自由度(绕虚铰3个方向相对转动)与一个多余约束(内力有一组非零解).

对4根连接链杆进行受力分析. 假设4根链杆 $A_{1} B_{1}$ , $A_{2} B_{2}$ , $A_{3} B_{3}$ , $A_{4} B_{4}$ 分别编号为1, 2, 3, 4; 取链杆1, 2为例：

链杆1与链杆2由链杆 $A_{1} A_{2}$ 与链杆 $B_{1} B_{2}$ 相连. 假设链杆 $A_{1} A_{2}$ 与链杆 $B_{1} B_{2}$ 的轴力对链杆1的合力为 $F_{12}$ . 由于 $A_{1} A_{2}$ 与 $A_{1} B_{2}$ 交于一点, 那么 $A_{1} B_{1}$ 与 $A_{2} B_{2}$ 共面, 因此存在唯一的交点 $P_{12}$ (当平行时交点为相应的无穷远点). 由牛顿第三定律, $F_{12} = - F_{21}$ , 且作用点均在 $P_{12}$ . 欲证明空间笛沙格定理, 仅需证明 $P_{12}, P_{13}, P_{14}, P_{23}, P_{24}, P_{34}$ 六点共面.

按照 $F_{12}$ 的定义方法定义 $F_{ij}, P_{ij} (i \neq j)$ .

对4根链杆列出平衡方程

$F_{12} + F_{13} + F_{14} = 0 (1)$

$F_{21} + F_{23} + F_{24} = 0 (2)$

$F_{31} + F_{32} + F_{34} = 0 (3)$

$F_{41} + F_{42} + F_{43} = 0 (4)$

分析方程(1)可以得出, 由于三力平衡, 因此3个力的作用线必然交于一点. 假设这个点为 $P_{1}$ ; 同理分析方程(2) $~$ (4)可以得出 $P_{2}, P_{3}, P_{4}$ .

根据上文分析, 由于 $F_{12}$ 作用点在 $P_{12}$ , 经过 $P_{1}, P_{2}$ , 因此, $P_{12}$ 在直线 $P_{1} P_{2}$ 上. 同理, 对于任意的 $i, j$ , $P_{ij}$ 在直线 $P_{i} P_{j}$ 上.

因此, 欲证明 $P_{12}, P_{13}, P_{14}, P_{23}, P_{24}, P_{34}$ 六点共面, 仅需证明 $P_{1}, P_{2}, P_{3}, P_{4}$ 四点共面.

由于 $F_{14}$ 作用线与 $P_{1} P_{4}$ 重合, $F_{13}$ 作用线与 $P_{1} P_{3}$ 重合, $F_{12}$ 作用线与 $P_{1} P_{2}$ 重合, 根据式(1), $P_{1} P_{4}$ 可以被 $P_{1} P_{3}$ 与 $P_{1} P_{2}$ 线性表出. 因此, $P_{4}$ 落在 $P_{1}, P_{2}, P_{3}$ 构成的平面上, $P_{1}, P_{2}, P_{3}, P_{4}$ 四点共面, $P_{12}, P_{13}, P_{14}, P_{23}, P_{24}, P_{34}$ 六点共面, 空间情形笛沙格定理得证.

4 结论

上文合理构造了平面杆件体系, 从结构力学几何组成分析的角度出发得到杆件体系几何可变的等价条件, 分析证明了射影几何中著名的笛沙格定理. 从中可见

(1)几何分析和内力分析的思路一致. 几何可变性分析的刚片取法和内力受力分析的隔离体取法一致, 但它们通过不同的理论各自推导到相同的结论. 这反映了结构力学中几何分析与受力分析的对偶性.

(2)铰接三角形规律和内力平衡方程均在拓广平面内有对应的表述, 这是证明进行的关键. 这反映了拓广平面— — 这一常用的射影平面模型是描述结构几何组成分析的合理的几何学模型^[7].

(3)在证明笛沙格定理过程中, 内力分析更能体现笛沙格定理的透视中心与透视轴的本质. 在高维情形的杆件体系构造中, 几何可变性已经不再是笛沙格定理条件和结论的等价条件, 但是, 内力存在非零解与否, 仍然对笛沙格定理的结构力学证明起到了关键作用.

(4)笛沙格定理是射影几何范畴内的定理, 经过射影变换后, 笛沙格定理仍然成立. 如果对该杆件体系进行射影变换, 两种分析证明仍然不变, 三线共点、三点共线的体系几何性质也不变. 这说明了杆件体系的多余约束存在性和几何可变性仍然不变, 这也反映了几何组成分析和射影几何之间深刻的内蕴联系.

The authors have declared that no competing interests exist.

参考文献

文献选项

1	Rankine WJM. On the application of Barycentric perspective to the transformation of structures. Philosophical Magazine, 1863, 26: 387-388 [本文引用:1]
2	Wunderlich W. Projective invariance of shaky structures. Acta Mechanica, 1982, 42(3-4): 171-181 [本文引用:1]
3	Crapo H, Whiteley W. Statics of frameworks and motions of panel structures: A projective geometric introduction. Structural Topology, 1982, 6(6): 43-82 [本文引用:1]
4	陈圣德. 笛沙格定理的几种证法与应用. 中学数学, 1981, 1: 14-19 [本文引用:1]
5	龙驭球, 包世华, 袁驷. 结构力学I ——基本教程. 第3版. 北京: 高等教育出版社, 2012 [本文引用:3]
6	龙驭球, 包世华, 袁驷. 结构力学II ——专题教程. 第3版. 北京: 高等教育出版社, 2012 [本文引用:1]
7	杨治林. 射影平面在结构几何组成分析中的应用. 力学与实践, 1999, 19(3): 57-58 [本文引用:2]
8	周建伟. 高等几何. 北京: 高等教育出版社, 2012 [本文引用:1]
9	冯克勤. 射影几何趣谈. 上海: 上海教育出版社, 1987 [本文引用:1]
10	袁承武. 四维空间的笛沙格定理及证明. 工程图学学报, 1985, 6(1): 47-49 [本文引用:1]

1863

0.0

... 1863年,Rankine^[1]提出了结构自由度的仿射不变性 ...

1982

0.0

... 1982年, Wunderlich^[2]从几何组成分析的角度阐明了结构的射影不变性 ...

1982

0.0

... 同年, Crapo等^[3]从受力分析的角度阐明了结构的射影不变性 ...

1981

0.0

陈圣德. 笛沙格定理的几种证法与应用. 中学数学, 1981, 1: 14-19

... 由于笛沙格定理深刻的对称性与几何学内涵,迄今为止,众多专家学者给出了许多种基于几何法或是综合法的证明^[4] ...

2012

0.0

... 依次构造平面和空间杆件体系,从几何组成分析与受力分析两个不同的角度,运用铰接三角形规律^[5]与零载法^[6], 在射影几何范畴内分析该种体系的几何组成^[7],证明了笛沙格定理的平面和空间两种情形,揭示了结构力学和射影几何的联系 ...

... 2 杆件体系的几何分析结构力学给出的平面几何组成分析铰接三角形规律有以下两种等价的表述形式^[5]： ...

... 根据结构力学理论^[5],铰接三角形规律在拓广平面内适用 ...

2012

0.0

1999

0.0

杨治林. 射影平面在结构几何组成分析中的应用. 力学与实践, 1999, 19(3): 57-58

... 这一常用的射影平面模型是描述结构几何组成分析的合理的几何学模型^[7] ...

2012

0.0

... 在此首先给出拓广平面的定义^[8] ...

1987

0.0

... 拓广平面满足如下两条重要性质^[9]: ...

1985

0.0

袁承武. 四维空间的笛沙格定理及证明. 工程图学学报, 1985, 6(1): 47-49

... 空间笛沙格定理^[10] 已知两个四点体的对应点的四条连线交于一点,那么这两个四点体的对应棱的6个交点在一个平面上 ...