横波引起的转动及其孪生剪切变形<sup>1)</sup>

引用本文

胡恒山. 横波引起的转动及其孪生剪切变形¹⁾ . 力学与实践, 2018,40(2): 207-209 复制到剪切板

Doi: 10.6052/1000-0879-17-331
Permissions

《力学与实践》编辑部所有

横波引起的转动及其孪生剪切变形¹⁾

胡恒山²⁾

哈尔滨工业大学航天科学与力学系,哈尔滨 150001

2) 胡恒山,教授,长期从事弹性动力学的教学与应用研究. E-mail: hhs@hit.edu.cn

收稿日期: 2017-09-25

资助项目: 1) 国家自然科学基金资助项目(11734017,11372091).

摘要

弹性介质中局部刚性转动的传播服从波动方程,其速度取决于介质的剪切模量和密度. 但是刚性转动不是介质的变形,为什么其速度依赖于表征形状变形恢复能力的剪切模量?本文证明横波传播过程中局部刚性旋转与剪切变形一一对应,互为依存. 发生刚性转动与剪切变形之后,微元体凭借剪切模量恢复其扰动前的形状,同时转回到扰动前的位置,这是转动可以传播且速度依赖于剪切模量的原因.

关键词: 局部刚性转动; 剪切变形; 横波速度; 剪切模量

中图分类号:O347,O42,P315,P631 文献标志码:A

文章图片

各向同性线性弹性介质中, 纵波是无旋的而横波是有旋的^{[1, 2]}. 在弹性波理论中, 旋转指微元体的刚性转动^{[2, 3, 4]}, 而横波速度取决于剪切模量和密度^{[1, 2]}. 转动不是变形, 剪切模量是介质抵抗变形并企图恢复到零偏应变状态的能力^{[3, 4]}, 旋转为什么能按横波速度传播呢?教材与文献均未解释. 横波与纵波是最基本的弹性波动形式, 导波、面波是以纵波和横波两种体波复合而成的. 鉴于横波在弹性波理论^{[1, 2]}、地震学^[5]、地震勘探^[6]、声波测井^[7]、超声检测^[8]和爆炸与冲击^[9]中占有重要地位, 有必要弄清楚横波引起转动的机制.

1 位移场的旋度及转动的传播

弹性力学告诉我们, 变形固体中一点的位移可分解为平移、局部刚性转动和变形3个独立的部分^{[1, 3, 4]}. 变形又分为体积变形和形状变形. 剪切模量反映介质抵抗形状变化的能力. 一点形状变形的程度, 可用偏应变来表征. 一点的切应变不为零, 该点的偏应变就一定不为零; 另一方面, 只要某点3个主应变方向上的线应变不完全相等, 该点就存在偏应变^{[10, 11]}, 这种情况下, 主方向之外的任意两个正交方向之间的切应变都不为0. 因此, 一点存在切应变和存在偏应变在本质上是相同的, 以下不再区分.

微元体上一点 $B$ 绕 $A$ 点转动所产生的位移 $d u$ , 可用旋转矢量 $ω$ 和从 $A$ 点到 $B$ 点的矢径 $d r$ 表示为^{[3, 4]}

${(d u)}_{r ot} = ω \times d r (1)$

而转动矢量为可用位移场的旋度表示^{[3, 4]}

${\pmb \omega } = \dfrac{1}{2}\nabla \times {\pmb u} \quad(2) $

与物体的整体刚体转动不同, 微元体的转动是局部的刚性转动, 下面简称为转动.

弹性波教材给出了如下转动矢量满足的波动方程^{[2, 11]}

$ \nabla ^2{\pmb \omega } - \dfrac{1}{c^2} \ddot {\pmb \omega } = {\bf 0}\, , \ \ c = \sqrt {\dfrac{\mu }{\rho }} \quad(3) $

式中$\ddot{\pmb\omega}$为角加速度. 式(3)表明, 转动按横波速度 $c$ 传播, 该速度取决于介质的剪切模量 $μ$ 和密度 $ρ$ .

弹性波能在弹性介质中传播, 是因为弹性介质具有两个特点：一是密度不为0, 运动的微元体有继续运动的惯性; 二是具有弹性恢复能力, 即微元体有恢复原有形态的能力. 打个比喻来说明吧, 将许多块砖沿一条直线排列, 让每一块砖立起来, 砖与砖的距离小于砖的高度. 现在以一定的水平速度推第一块砖的顶部, 这块砖由于惯性就向前方倾斜, 在打击相邻的砖后倒下; 第二块砖也由于惯性而向前方倾斜, 在打击第三块砖后倒下; 依次, 直到最后一块砖倾倒. 但这样的多米诺效应不是弹性波, 因为这些砖倾倒后没有能力恢复到直立状态, 不能在平衡位置来回摆动. 令人不解的是, 剪切模量表征介质抵抗偏应变(或切应变)并企图恢复形状的能力, 而转动是局部的刚性运动而不是变形, 转动的传播速度为什么依赖于剪切模量呢?

2 平面横波引起的旋转及其孪生的剪切变形

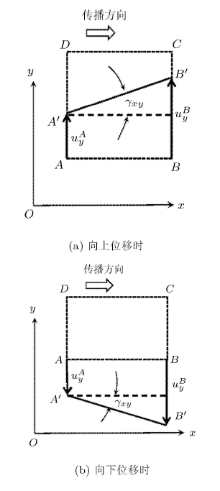
本节针对各向同性线弹性介质中的平面横波, 证明局部转动的传播必然伴生偏应变. 或者说, 横波不可能只产生转动而不引起偏应变. 图1(a)显示横波在某点 $A$ 附近引起的位移. 按定义, 横波传播时, 位移方向与传播方向垂直. 设均匀平面横波沿 $x$ 方向传播, 那么图中各点均只有 $y$ 方向位移, 且波阵面( $x$ 等于常数的平面, 它与 $xy$ 平面的交线为一条竖直线)上各点的位移相同. 考察闭合路径 $ABCDA$ , 记 $Δ x = x^{B} - x^{A}$ , $Δ y = y^{D} - y^{A}$ . 位移沿该路径的环量为 $u_{y}^{B} Δ y - u_{y}^{A} Δ y$ , 该路径包围的面积为 $Δ x Δ y$ , 其上的位移环量面密度即为该点的旋度, 其值为

${(\nabla \times u)}_{z} = \lim_{Δ x \to 0, Δ y \to 0} (u_{y}^{B} Δ y - u_{y}^{A} Δ y) / (Δ x Δ y) =$

$\lim_{Δ x \to 0} (u_{y}^{B} - u_{y}^{A}) / Δ x (4)$

	Figure Option View Download New Window
	图1 平面横波引起的位移

注意到原来的直角 $∠ BAD$ 变形后成为斜角 $∠ B' A' D$ . 按照定义^[10], 这个角度减小量就是切应变, 其值正好等于式(4)的右侧表达式. 另一方面, 按式(2)的定义, 式(4) 的左端等于平面内转动量的2倍. 可见

$γ_{xy} = 2 ω_{z} (5)$

此式表明：平面横波引起转动时, 一定引起切应变. 对于 $u_{y}^{B} < u_{y}^{A}$ 的情况, 切应变 $γ_{xy}$ 将为负值, 而转动量也是负值, 式(5)仍然成立.

波的传播引起微团振动, 前半个周期的位移与后半个周期的位移指向可以不同. 图1(b)显示横波在某点 $A$ 附近引起向下的位移. 沿闭合路径 $ABCDA$ , 位移的环量仍为 $u_{y}^{B} Δ y - u_{y}^{A} Δ y$ , 但这里 $u_{y}^{B}$ 和 $u_{y}^{A}$ 都是负数. 该路径包围的面积为 $Δ x Δ y$ . 计算位移环量面密度, 得到该点的旋度, 其值仍可用式(4)表达, 而图中切应变也为负值. 式(5) 依然成立.

以上为图示方便, 按均匀平面横波进行了推导. 但式(5)对于非均匀平面横波也成立. 事实上, 对于沿 $x$ 方向传播的横波, 必有 $u_{x} = 0$ , 于是切应变 $γ_{xy} = \partial u_{y} \partial x + \partial u_{x} \partial y = \partial u_{y} \partial x$ , 局部刚体转动为 $ω_{z} = 12 (\partial u_{y} \partial x - \partial u_{x} \partial y) = 12 \partial u_{y} \partial x$ , 即得 $γ_{xy} = 2 ω_{z}$ , 这正是式(5).

式(5)是针对平面横波推导出来的, 一般的横波不一定满足该式. 不过, 由于任一横波总可以表达成平面横波的组合, 而每个平面横波引起孪生的切应变与转角, 可得出结论：弹性横波一定既引起旋转又引起剪切变形.

纵波引起切应变, 但不引起转动. 因此, 式(5)揭示了横波特有的一种关系：转动与切应变一一对应, 相互依存.

既然横波引起转动时必然引起切应变, 局部转动发生后, 要恢复到转动前的状态, 就必须同时将微元体恢复到零切应变状态, 即恢复到原来的形状. 转动是局部的刚性运动, 它自身不是变形, 介质似乎没有恢复转动的因素; 但转动与剪切变形是孪生的, 介质能否恢复到转动前的状态, 就取决于形状能否恢复, 即取决于介质的剪切模量. 这就解释了转动为什么可以传播, 且传播速度依赖于剪切模量.

3 纵波引起的剪切变形

在作者的前一篇文章^[12]中, 证明并举例说明了纵波一定引起偏应变. 而一点出现偏应变就意味着该点发生了形状的改变, 除主应变方向外的其他任意两个正交方向之间的切应变都不为0. 在本文的这个姊妹篇中作者还指出, 纵波速度之所以不仅依赖于体积模量而且依赖于剪切模量, 是因为纵波扰动引起了体积变形和形状改变. 纵波可在弹性固体介质中传播是因为介质既有恢复体积变形的能力, 又有恢复剪切变形的能力, 前者由体积模量表征, 后者由剪切模量表征. 传播速度依赖于介质受扰动后的恢复能力, 所以纵波速度公式中既出现了体积模量又出现了剪切模量.

体积变形与剪切变形同时发生于纵波. 纵波引起扰动后, 介质必须既恢复体积又恢复形状才能回复到平衡位置, 这就决定了纵波速度公式必须同时含有体积模量和剪切模量. 即使单独考察体应变的传播, 其速度也等于既依赖于体积模量又依赖于剪切模量的纵波速度. 类似地, 形状变化与刚性转动都发生于横波. 横波引起扰动后, 介质必须既恢复形状又使转角消失, 才能回复到平衡位置. 因横波引起的形状变化与刚性转动同步发生也同步消失, 横波速度就依赖于剪切模量了. 即使单独考察转动的传播, 其速度也是依赖于剪切模量的.

偏应变或切应变(及相应的形状改变)既可由纵波引起, 又可由横波引起. 它伴随体应变(及相应的体积改变)出现于纵波中, 伴随转动出现于横波中. 为了方便记忆, 打个通俗的比方吧. 偏应变可拥抱“ 体应变” 乘快艇(纵波)冲浪, 也可牵手“ 转动” 在慢速度的游船(横波)上游玩.

与剪切既发生于横波又发生于纵波不同, 局部刚性转动只发生于横波. 纵波虽然引起剪切, 但纵波是无旋波, 位移场的旋度为0, 不引起转动.

4 结论

(1)横波引起局部刚性转动和剪切变形, 且转动和剪切一一对应, 相互依存. 这是横波特有的性质.

(2)既然横波引起的转动与切应变同步发生, 那么要恢复到转动前的状态就必须恢复形状; 而形状的恢复取决于剪切模量. 所以转动以横波速度传播.

(3)形状改变可由纵波引起, 也可由横波引起. 但转动不会出现于纵波.

The authors have declared that no competing interests exist.

参考文献

文献选项

1	Achenbach JD. Wave Propagation in Elastic Solids. Amsterdam: North-Holland Publishing Company, 1973 [本文引用:4]
2	Eringen AC, Suhubi ES. Elastodynamics, v2, Linear Theory. New York: Academic Press, 1975 [本文引用:5]
3	王敏中, 王炜, 武际可. 弹性力学教程(修订版) 北京: 北京大学出版社, 2011 [本文引用:5]
4	陈明祥. 弹塑性力学. 北京: 科学出版社, 2007 [本文引用:5]
5	Aki K, Richards PG. Quantitative Seismology. Second Edtion. Sauslito, California: University Science Books, 2002 [本文引用:1]
6	何樵登. 地震勘探原理和方法. 北京: 地质出版社, 1986 [本文引用:1]
7	王克协, 崔志文. 声波测井新理论和方法进展. 物理, 2011, 40(2): 88-98 [本文引用:1]
8	Rose JL. Ultrasonic Waves in Solid Media. New York: Cambridge University Press, 2014 [本文引用:1]
9	宁建国. 爆炸与冲击动力学. 北京: 国防工业出版社, 2010 [本文引用:1]
10	粟一凡. 材料力学, 下册, 第2版. 北京: 高等教育出版社, 1960 [本文引用:2]
11	杜庆华, 余寿文, 姚振汉. 弹性理论. 北京: 科学出版社, 1986 [本文引用:2]
12	胡恒山. 拉梅常数的力学意义与剪切模量出现于纵波速度公式的原因. 地球物理学进展, 2018, 33(1): 219-222 [本文引用:1]

1973

0.0

... 各向同性线性弹性介质中,纵波是无旋的而横波是有旋的^[1,2] ...

... 在弹性波理论中,旋转指微元体的刚性转动^[2,3,4],而横波速度取决于剪切模量和密度^[1,2] ...

... 鉴于横波在弹性波理论^[1,2]、地震学^[5]、地震勘探^[6]、声波测井^[7]、超声检测^[8]和爆炸与冲击^[9]中占有重要地位,有必要弄清楚横波引起转动的机制 ...

... 1 位移场的旋度及转动的传播弹性力学告诉我们,变形固体中一点的位移可分解为平移、局部刚性转动和变形3个独立的部分^[1,3,4] ...

1975

0.0

... 各向同性线性弹性介质中,纵波是无旋的而横波是有旋的^[1,2] ...

... 在弹性波理论中,旋转指微元体的刚性转动^[2,3,4],而横波速度取决于剪切模量和密度^[1,2] ...

... 弹性波教材给出了如下转动矢量满足的波动方程^[2,11] ...

2011

0.0

... 在弹性波理论中,旋转指微元体的刚性转动^[2,3,4],而横波速度取决于剪切模量和密度^[1,2] ...

... 转动不是变形,剪切模量是介质抵抗变形并企图恢复到零偏应变状态的能力^[3,4],旋转为什么能按横波速度传播呢?教材与文献均未解释 ...

... 1 位移场的旋度及转动的传播弹性力学告诉我们,变形固体中一点的位移可分解为平移、局部刚性转动和变形3个独立的部分^[1,3,4] ...

... 微元体上一点 B绕 A点转动所产生的位移 du,可用旋转矢量 ω和从 A点到 B点的矢径 dr表示为^[3,4] ...

... 而转动矢量为可用位移场的旋度表示^[3,4] ...

2007

0.0

... 在弹性波理论中,旋转指微元体的刚性转动^[2,3,4],而横波速度取决于剪切模量和密度^[1,2] ...

... 转动不是变形,剪切模量是介质抵抗变形并企图恢复到零偏应变状态的能力^[3,4],旋转为什么能按横波速度传播呢?教材与文献均未解释 ...

... 1 位移场的旋度及转动的传播弹性力学告诉我们,变形固体中一点的位移可分解为平移、局部刚性转动和变形3个独立的部分^[1,3,4] ...

... 微元体上一点 B绕 A点转动所产生的位移 du,可用旋转矢量 ω和从 A点到 B点的矢径 dr表示为^[3,4] ...

... 而转动矢量为可用位移场的旋度表示^[3,4] ...

2002

0.0

1986

0.0

2011

0.0

王克协, 崔志文. 声波测井新理论和方法进展. 物理, 2011, 40(2): 88-98

2014

0.0

2010

0.0

1960

0.0

... 另一方面,只要某点3个主应变方向上的线应变不完全相等,该点就存在偏应变^[10,11],这种情况下,主方向之外的任意两个正交方向之间的切应变都不为0 ...

... 按照定义^[10],这个角度减小量就是切应变,其值正好等于式(4)的右侧表达式 ...

1986

0.0

... 弹性波教材给出了如下转动矢量满足的波动方程^[2,11] ...

2018

0.0

胡恒山. 拉梅常数的力学意义与剪切模量出现于纵波速度公式的原因. 地球物理学进展, 2018, 33(1): 219-222

... 3 纵波引起的剪切变形在作者的前一篇文章^[12]中, 证明并举例说明了纵波一定引起偏应变 ...