海上漂浮软管是浮式生产储卸油装置上外输系统的关键设备.漂浮软管结构复杂且常年漂浮于海面上,极易受到风、浪、流等环境载荷的作用产生疲劳破坏而造成原油泄漏.首先,采用ABAQUS软件,建立了软管的有限元模型,得到了漂浮软管在弯矩和内压作用下的有限元结果;其次,采用水平方向的Morison方程和风载荷来描述漂浮软管在海面上复杂的载荷情况;再次,将静力学分析结果导入到FE-Safe疲劳分析软件中,将节点应力结果作为时间载荷历程,乘以相应的载荷倍数,得到疲劳分析的载荷谱,载入此载荷谱计算,得到了漂浮软管的寿命分布云图,其最小寿命满足工程要求;最后,分析了内压对疲劳寿命的影响,结果表明,一定大小的内压能提高软管的疲劳性能.
The bonded floating hose is a key equipment for the floating production storage and offloading unit (FPSO). The hose has a very complex structure, floating on the sea surface, subjected to wind, wave and current load. First of all, ABAQUS is used to build a finite element model, and a case under the bending moment and the internal pressure is analyzed. Secondly, the modified horizontal Morison equation and the wind load are used to describe the complex load condition. The above static analysis results are used by the FE-Safe fatigue analysis software as the input. The load spectrum is acquired by multiplying the node stress results with the corresponding load ratio. Then the life distribution contour of the hose is obtained. The calculated minimum fatigue life meets the engineering requirements. Finally, the effect of the internal pressure on the fatigue life is considered. The results show that the certain internal pressure can improve the fatigue performance of the hose.
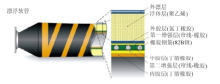
漂浮软管是浮式生产储卸油装置(floating production storage offloading, FPSO)上外输系统的长线关键设备, 是原油外输的重要通道, 也是FPSO生产管理中不可或缺的重要装备[1].漂浮软管单根长10$\sim$12m, 通过端部法兰连接成管串, 在海上铺设完成后, 一端连接浮筒, 一端连接FPSO, 在服役期间常年漂浮于海面上, 如图1(a)所示.漂浮软管重量轻、抗弯刚度小, 所受到的浮力较大.漂浮软管长期处在风、浪、流等复杂的环境载荷作用下, 会产生交变运动, 导致疲劳破坏[2], 引起原油泄漏, 造成巨大的经济损失.因此, 漂浮软管的疲劳性能对于海上原油输送安全至关重要.图1(b)所示为某漂浮软管由疲劳破坏导致的橡胶层裂纹[3].漂浮软管正常输油期间, 其工况为内部承受油流压力, 外部承受风、浪、流等环境载荷, 使漂浮软管产生一定大小的弯矩.基于此本文以百年一遇海况对漂浮软管进行了疲劳寿命分析.
漂浮软管为多层复合结构, 属于粘结型软管. 其结构形式如图2所示.由内至外依次为内胶层、第一增强层、中胶层、第二增强层、外 胶层.其中内胶层、中胶层材料为丁腈橡胶, 外胶层为氯丁橡胶. 中胶层中嵌入单根螺旋形式的缠绕钢筋, 螺旋钢筋材料为82B钢.第一增强层和第二增强层分别由14层和2层各向异性的帘线-橡胶复合材料组成, 帘线布置以+55° 和-55° 交替铺设而成.外胶层外有聚乙烯材料所组成的浮体层, 为整根软管提供浮力.
漂浮软管越来越多地应用于近海原油输送工程中, 也因此吸引了国内外学者对其力学性能的研究. Tang 等[4]采用七种模型及对应的有限元模型研究了柔性软管抗拉层螺旋线在弯曲作用下的应力分布规律, 并分析了七种模型的有效性和局限性.Tang 等[5]采用等效应变能法研究了柔性软管内骨架层在外压下的的压溃屈曲. Roveri等[6]借助数值软件Ocraflex, 对漂浮软管在连接FPSO和浮筒作业时的整体受力情况作了分析. Silva等[7]利用接触模型分析了漂浮软管在安装、作业时产生的非线性动力学问题, 对指导漂浮软管的安装具有一定的实际应用价值.Gonzalez等[8]采用软件Rebar建模的方法研究了漂浮软管在轴向载荷和弯曲载荷下的力学响应, 给出了关键截面的应力和变形情况.以上研究主要针对漂浮软管在简单载荷下的力学响应, 国内外学者对漂浮软管疲劳寿命的研究较少. Lassen 等[9]利用软件Ocraflex先进行了漂浮软管的整体受力分析, 得出了危险截面的位置, 然后分析了该位置的疲劳破坏情况.Lassen等[10]研究了漂浮软管在内压、拉伸和弯曲反复作用下的极限承载力和疲劳寿命, 采用了有限元和全尺度试验的方法来说明该漂浮软管符合API 17K等相关规范的要求.
为了研究漂浮软管的疲劳寿命, 首先, 对软管进行静态的有限元分析, 得到弯矩和内压作用下的应力应变结果, 将此节点应力结果作为时间载荷历程输入到疲劳分析软件中; 其次, 得到相关材料的SN曲线, 以此作为材料疲劳性能的重要参数导入到疲劳分析软件中; 再次, 对漂浮软管复杂的风、浪、流载荷进行分析, 得到加持在软管上的疲劳载荷, 乘以相应的载荷倍数, 得到疲劳分析的载荷谱, 将其导入到疲劳分析软件中; 最后, 对漂浮软管的使用寿命进行了仿真分析.
首先对漂浮软管进行静态有限元分析, 建立了漂浮软管的有限元模型, 划分得到网格和节点信息, 并计算得到在静载荷作用下各节点上的应力应变结果, 从而可以在疲劳分析时将此应力应变结果作为载荷时间历程.
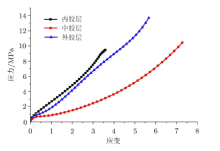
漂浮软管的外胶层材料为氯丁橡胶, 中胶层和内胶层为丁腈橡胶.由于橡胶的材料属性和其组分、加工工艺等密切相关, 中胶层和内胶层虽同为丁腈橡胶, 但由于其各组分含量不同, 故其力学性能也不同.因此, 为了选择合适的橡胶本构模型, 需要分别对软管的三层橡胶层进行单轴拉伸试验, 选取宽度6mm, 标距25mm的不同厚度的试样, 以500mm/min的加载速率分别进行四组试验, 综合考虑不同变形范围内的曲线拟合效果, 其应力应变曲线如图3所示, 选取三阶Odgen形式的本构, 其应变能函数为[11]
$ W = \sum_{n = 1}^N \dfrac{\mu _n }{\alpha _n }\left[ {J^{\tfrac{ - \alpha _n }{3}}\left( {\lambda _1^{\alpha _n } + \lambda _2^{\alpha _n } + \lambda _3^{\alpha _n } } \right) - 3 +}\right. \\ \qquad \left.{ 4.5K\left( {J^{\tfrac{1}{3}} - 1} \right)^2} \right] \quad(1)$
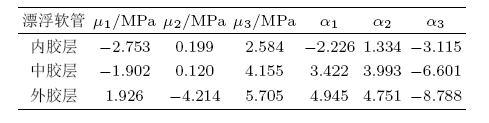
式中, $\mu _n$, $\alpha _n $为材料参数; $K$为初始体积模量; $J$为体积率, 对不可压缩材料$J = 1$.材料参数如表1所示.
| 表1 各橡胶材料参数 |
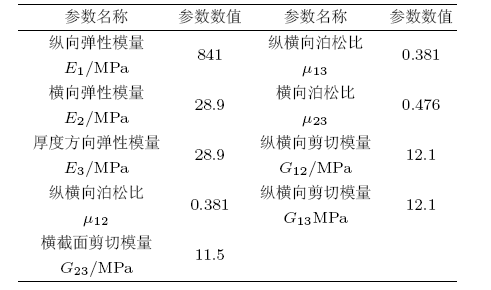
螺旋钢筋材料选用82B高碳钢, 端部配件材料为Q235钢, 增强层材料为聚酯帘子线, 其材料参数如 表2所示.
| 表2 帘布橡胶材料的工程弹性常数 |
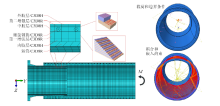
漂浮软管是由多层材料组成的粘结型结构, 在有限元软件Abaqus中, 先建立整根管体的模型, 然后用Partition命令将整根管体分割为多层结构, 无需设置层间绑定约束, 且保证了受力和变形的连续性.各层分别赋予不同的材料属性, 其中橡胶选择超弹性模型. 采用Embedded约束命令将螺旋钢筋嵌入到中胶层.增强层的铺设选用Composite layup工具, 在其中设置铺层厚度和角度.
在模型中, 虽然只是对1.5m的中间管段和一端的端部配件进行分析, 但是两端的端部约束状态可以参考实际管道的刚性约束.在 建立的管道模型的顶面和底面各建立一个参考点, 将管道端面的所有节点自由度与参考点进行耦合.漂浮软管底部参考点的六个自由度完全约束, 顶部参考点施加弯矩载荷, 其方向为垂直于软管轴向, 沿整体坐标系下$Z$轴负向, 大小为50kN$\cdot$m, 具体如图4所示. 内压1.5MPa施加于管道内壁.划分网格时, 橡胶层采用杂交单元C3D8H, 加强层、螺旋钢筋和端部配件采用线性减缩积分单元C3D8R.最终单元数为47 798个, 节点数为71 241个.
在进行疲劳分析时, 输入单位加载的节点应力结果, 然后把该节点应力结果作为时间载荷历程, 乘以相应的载荷倍数, 设计出疲劳载荷谱, 从而求出疲劳寿命.因此FE-Safe分析的主要步骤是接受ABAQUS的静力分析结果, 包括节点数、单元数、节点应力值等, 在此基础上定义疲劳载荷历程和材料系数, 最后得到疲劳分析的结果.
线性累计损伤理论是指试件在循环载荷的作用下, 疲劳损伤的程度与载荷循环的次数是线性变化, 而且疲劳损伤可线性累加, 各个应力之间相互独立、互不相关, 当累加的损伤达到某一数值时, 试件即会发生疲劳破坏[12].在线性累积损伤理论中最为经典的就是Miner-Palmgren理论[13].
Miner理论中, 构件在疲劳载荷下, 一个循环所造成的损伤 $D = 1 / N$, 其中$N$为对应于当前载荷水平的疲劳寿命.等幅载荷下$n$个循环所造成的损伤 $D = n / N$. 变幅载荷下$n$个循环所造成的损伤
式中, $N_i $为对应于当前载荷水平的疲劳寿命. 当构件达到临界疲劳损伤$D = D_{\rm CR} = 1$时认为发生疲劳破坏.
材料的SN曲线是指以材料标准试件疲劳强度为纵坐标, 以疲劳寿命的对数值为横坐标, 在一定循环特征下标准试件的疲劳强度与疲劳寿命之间关系的曲线, 也被称为应力-寿命曲线.SN曲线是衡量材料疲劳性能的重要指标, 也是计算材料疲劳寿命必不可少的重要参数.构件疲劳寿命的计算是建立在材料SN曲线的基础之上的.
FE-Safe软件的材料数据系统管理中具有丰富的钢、铝合金等材料数据, 以及一个独立的橡胶分析模块Endurica模块, 此模块中包含丰富的橡胶材料参数, 可以用来分析橡胶材料的疲劳性能.此外, FE-Safe在数据库中含有Seeger材料近似算法, 允许利用材料的抗拉强度 和弹性模量生成近似的保守的材料疲劳数据.
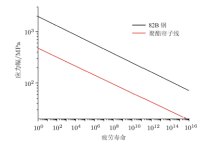
漂浮软管中螺旋钢筋采用82B碳钢, 可从FE-Safe自带的材料数据系统中找到相对应的材料.增强层材料为聚酯帘子线, 采用FE-Safe中的Seeger材料近似算法, 根据试验测得的聚酯帘子线的弹性模量为384MPa, 抗拉强度为 317MPa, 可得出聚酯帘子线的近似的保守的SN曲线. 如图6所示.
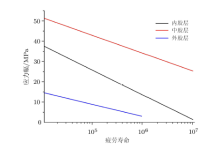
外胶层材料为氯丁橡胶, 中胶层和外胶层为丁腈橡胶. 橡胶的材料参数通过加载FE-Safe中的Endurica模块可得出.三层橡胶层的SN曲线如 图7所示.
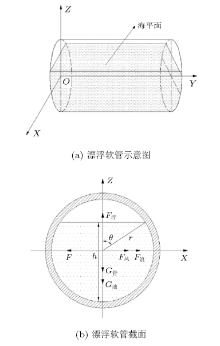
漂浮软管在工作期间始终漂浮于海面上, 部分柱体浸没在海水中, 部分柱体裸露在海面上, 如图8(a)所示. 其受力分析示意图如图8(b)所示, 水平方向上, 海面上部分受到风载荷作用, 海面以下部分受到波浪载荷作用; 竖直方向上, 软管受到的浮力与软管的重力和软管内运输油的重力之和相等, 即满足
$\left.\begin{array}{l} F = F_{\hbox{风}} + F_{\hbox{浪}}\\ F_{{浮}} = G_{{管}} + G_{\hbox{油}} \end{array}\right\} \quad(3) $
式(3)中, $F_{\hbox{浪}}$表示波浪力, $F_{\hbox{风}}$表示作用在软管上的风载荷, 可按下式[14]进行计算
$F_{\hbox{风}}= KK_{\rm Z} p_0 A \quad (4)$
$p_0 = \alpha v_{\rm i}^2 \quad (5)$
式中,$K$为风载荷形状系数,对圆柱体侧壁来说取0.5;$A$为受风面积;$K_{\rm Z} $为海上风压高度变化系数,取1.0;$p_0 $为基本风压;$\alpha $为风压系数,取 0.613N$\cdot$s$^2$/m$^4$;$v_{\rm i} $为设计风速,考虑重现期$100a$和3s阵风时,最大风速为64.7m/s.
在工程上, 计算和波长相比尺度较小的细长柱体(对于圆柱体, $D / L < 0.2$)的波浪力仍广泛采用莫里森方程[15]
$f_{\rm H} = f_{\rm D} + f_{\rm I} \quad(6)$
式中, $f_{\rm D}$表示流体流过桩柱时由于黏性作用与柱体产生的阻力和在柱后尾流中产生的漩涡而引起的阻力, 又叫做速度力, 可表示为
$f_{\rm D} = \dfrac{1}{2}C_{\rm D} \rho A_0 u_x \left| {u_x } \right| \quad(7)$
式中, $u_x $为该处水质点的水平速度; $A_0 $为单位柱高在垂直于波向上的投影面积; $\rho $为海水密度; $C_{\rm D}$为垂直于柱体轴线方向的拖曳力系数.
$f_{\rm I}$ 表示流体流过桩柱时的惯性力, 可表示为
$f_{\rm I} = \rho V_0 \dfrac{d u_x }{d t} + C_{\rm m} \rho V_0 \dfrac{d u_x }{d t} = C_{\rm M} \rho V_0 \dfrac{d u_x }{d t} \quad(8)$
式中, $\dfrac{d u_x }{d t}$为水平加速度; $V_0 $为单位柱高的排水体积; $C_{\rm m} $为附加质量系数; $C_{\rm M}$为质量系数. 以上是直立柱体上的波浪力的计算公式.对于水平柱体, 可将上述莫里森方程推演至矢量形式, 从而得到倾斜柱体上的莫里森方程, 进而求得水平柱体上的波浪力为
$ \left\{ \!\!\begin{array}{l} f_x \\ f_y \\ f_z \end{array} \!\! \right\} = \dfrac{1}{2}C_{\rm D} \rho A_0 \left\{ \!\!\begin{array}{l} \sin ^3\psi \\ \sin ^2\psi \cos \psi \\ 0 \end{array} \!\! \right\}u_x^2 + \\ \qquad C_{\rm M} \rho V_0 \left\{ \!\! \begin{array}{l} \sin ^2\psi \dfrac{\partial u_x }{\partial t} \\ - \sin \psi \cos \psi \dfrac{\partial u_x }{\partial t}\\ - \dfrac{\partial u_z }{\partial t} \end{array}\!\! \right\} \quad(9) $
式中, $\psi $为水平柱体轴线方向与波浪传播方向的夹角.
由式(4)和式(9)可看出:绕流拖曳力与柱体在垂直于波浪传播方向上的投影面积有关; 绕流惯性力与柱体的排水体积有关[16]; 对于海面上部分柱体, 所受到的风载荷也与海面以上部分的投影面积有关.
根据软管竖直方向受力平衡, 可有
$\begin{array}{1} A_0 L_1 \rho = \pi \left( {\dfrac{D}{2} - d_{\rm t} } \right)^2L_1 \rho _{\hbox{油}} +\\ \qquad \pi \left[ {\left( {\dfrac{D}{2}} \right)^2 - \left( {\dfrac{D}{2} - d_{\rm t} } \right)^2} \right]L_1 \rho _{\hbox{管}} \end{array}\quad(10) $
式中, $L_1 $为软管长度; $\rho $为海水密度; $\rho _{\hbox{油}}$和$\rho _{\hbox{管}}$分别为所输送油的密度和软管密度; $D$为管子外径; $d_{\rm t} $为软管厚度.又根据几何关系可得到处于海面下的软管截面面积为
$\begin{array}{1} A_0 = \dfrac{2\pi - 2\theta }{2\pi }\pi \left( {\dfrac{D}{2}} \right)^2 +\\ \qquad \left( {h - \dfrac{D}{2}} \right)\sqrt {\left( {\dfrac{D}{2}} \right)^2 - \left( {h - \dfrac{D}{2}} \right)^2} =\\ \qquad \left( {\pi - {\rm arc}\cos \left[ {\left( {h - \dfrac{D}{2}} \right) \Bigg / \dfrac{D}{2}} \right]} \right)\left( {\dfrac{D}{2}} \right)^2 +\\ \qquad \left( {h - \dfrac{D}{2}} \right)\sqrt {\left( {\dfrac{D}{2}} \right)^2 - \left( {h - \dfrac{D}{2}} \right)^2} \end{array}\quad(11) $
联立式(10)和式(11) 可求得软管截面被海水所淹没的高度$h$及截面面积$S$.由此可得出, 漂浮软管单位长度水平方向所受载荷为
$ \begin{array}{1} F = \dfrac{1}{2}C_{\rm D} \rho h\sin ^3\psi u_x^2 + C_{\rm M} \rho A_0 \sin ^2\psi \dfrac{\partial u_x }{\partial t}+\\ \qquad KK_{\rm Z} p_0 \left( {\dfrac{\pi D^2}{4} - A_0 } \right) \end{array}\quad(12) $
以百年一遇海况下输送原油为例, 软管密度为 879.18kg/m$^{3}$, 海水密度取1025kg/m$^{3}$, 输送原油密度为928kg/m$^{3}$, 波浪的相关参数如表3所示.
| 表3 波浪参数 |
根据波浪理论[17]应用划分依据, 当$d / L > 0.2$, 且$H / d \leqslant 0.2$, 使用线性波理论.依据线性波理论[18], 水质点沿水深的速度和加速度的分布为
$\left.\begin{array}{1} u_x = k\dfrac{ag}{\omega }\dfrac{\cosh \left[ {k\left( {z + d} \right)} \right]}{\cosh kd}\cos \left( {kx - \omega t} \right) \\ \dfrac{\partial u_x }{\partial t} = kag\dfrac{\cosh \left[ {k\left( {z + d} \right)} \right]}{\cosh kd}\sin \left( {kx - \omega t} \right) \end{array}\right\} \quad(13) $
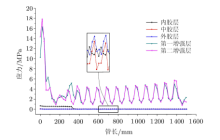
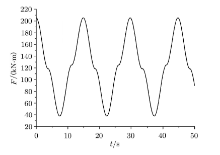
式中, $a$为振幅; $k$为波数; $\omega $为频率. 依据相关文献[19], 取拖曳力系数$C_{\rm D} =1.2$, 质量系数$C_{\rm M} = 2$. 将以上各参数代入式(12)中, 计算可得到漂浮软管受到的水平载荷如图9所示.
疲劳分析的有限元模型建立完成后, 将本文的有限元模型计算结果与四组试验数据[20]进行对比, 以验证有限元模型的准确性.在有限元模型中, 设定模型的边界条件与试验的边界条件一致, 得到有限元结果和试验结果的对比, 如表4所示.
| 表4 有限元计算结果和试验结果 |
从上表中可看出有限元计算结果和试验结果的误差在疲劳寿命分析误差的可接受范围内, 基本可认为该有限元模型能较准确地预测橡胶漂浮软管的疲劳寿命, 即所建立的有限元模型是有效、可靠的.
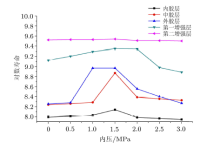
在内压和弯矩共同作用下漂浮软管疲劳对数寿命最小值出现在内胶层, 分析结果如图10所示, 从图中可看出疲劳寿命最小为$10^{8.140}$h(约为67年), 满足工程上设计寿命系数至少为10的要求(软管设计寿命6年).其中, 寿命最小的位置出现在管子的端部, 这是由于端部的应力集中所导致的橡胶的应变较大, 从而导致寿命较低.此外, 还发现寿命云图也呈现较为明显的周期特征, 条纹分布间距和螺旋钢筋的螺距大致相同, 寿命较低的位置还出现在螺旋钢筋缠绕的位置, 这是由于钢筋和橡胶的弹性模量相差较大, 导致橡胶产生较大的应变梯度, 从而引起寿命的下降.
(1)建立了漂浮软管的有限元模型, 得到了漂浮软管在有内压和弯矩作用下的静态分析结果.
(2)分析了海洋漂浮软管所受的载荷情况, 采用水平方向的Morison方程和风载荷来描述软管的受力情况, 并采用线性波理论, 得到了漂浮软管的载荷谱.
(3)在此基础上, 建立了漂浮软管疲劳寿命分析模型, 载入载荷谱和材料的SN曲线进行计算, 得到了软管的疲劳寿命, 其最小寿命满足工程要求.
(4)分析了内压对疲劳寿命的影响, 指出一定内压的存在对漂浮软管的疲劳性能有较大的提升.
The authors have declared that no competing interests exist.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|