设计磁流变六杆隔振平台,以改善星箭界面低频振动环境.采用牛顿-欧拉法建立整星隔振平台动力学模型,利用固定界面模态综合法得到卫星和隔振平台动力学模型.由于星箭界面低频振动环境在特定频段存在振动量级较大的问题,采用频域加权LQR (linear quadratic regulator)方法,利用直接分解法扩展系统状态变量,进行磁流变阻尼器半主动控制系统设计.仿真结果表明,相对传统控制方法,频域加权LQR方法在特定频段减振效果明显改善,且在其他频段没有恶化,验证了算法有效性.
To improve the interface vibration environment of the satellite and the rocket,a magnetorheological six-pole vibration isolation platform is designed. The dynamic model of the satellite vibration isolation platform is established by using the Newton-Euler method. The dynamic model of the satellite and the vibration isolation platform is built by using the fixed interface modal synthesis method. In order to study the specific frequency band attenuation, the frequency-shaping LQR (linear quadratic regulator) method which extends the system state variables by direct decomposition is used to design the semi-active control system of magnetorheological damper. The simulation results show that the frequency-shaping LQR method is better than the traditional control method, and the control effect is not deteriorated in other frequency bands. The effectiveness of the algorithm is verified.
在卫星的整个寿命周期内, 其在发射过程中经受的振动环境最为恶劣, 这期间航天器要经受各种不同形态的准静态载荷及时变动载荷的作用. 恶劣的振动环境往往是造成卫星发射失败的主要原因. 在不改变卫星结构的前提下, 在锥壳适配器与卫星之间加入Stewart六杆隔振平台, 以减小卫星发射时所承受的环境载荷, 降低对卫星及其设备的动态性能的要求.
隔振平台采用磁流变阻尼器作为半主动控制器件, 由于磁流变阻尼器所需能量少, 具有较大的阻尼力调节范围, 目前已经在航空、船舶、机械和土木等领域取得了一定的应用[1, 2, 3, 4]. 同时, 国内外对基于磁流变阻尼器的整星隔振平台做了相关研究工作$^{[5\hbox{-}7]}$, 仿真与试验结果表明, 半主动隔振平台可以取得较好的低频隔振效果.
对磁流变阻尼器系统控制一般采用双层控制策略, 即分为外层和内层控制, 外层控制根据系统模型的特征得到期望阻尼力, 使系统控制效果满足要求, 外层控制器不需要考虑执行机构的执行能力, 即按照主动控制的方式进行计算, 外层控制算法主要包括天棚控制算法、最优控制、自适应控制、智能控制等[8, 9]; 内层控制算法的作用是使磁流变阻尼器的输出阻尼力快速跟踪期望阻尼力, 但是由于磁流变阻尼器能够提供的阻尼力方向与激励性质相关, 并不完全依赖于控制电流, 因而实际阻尼力并不能完全跟踪期望阻尼力, 内层控制算法主要有开关控制、神经网络控制、模糊控制等[10, 11].由于我国运载火箭星箭界面振动环境在特定频段存在振动量级较大的问题, 采用频域加权LQR (linear quadratic regulator)方法[12, 13, 14], 对特定频段振动进行重点衰减.文献[12, 13, 14]针对汽车主动悬架系统, 通过频域加权LQR方法对人体敏感的频率区间进行振动控制, 取得了很好的抑制效果, 但由于采用串联分解法扩展状态变量, 其选取的加权函数特征方程不能存在复数解, 因而很难选取合适的加权函数, 本文通过采用直接分解法, 使特征方程只需满足稳定性条件即可, 从而降低加权函数选取难度, 并通过仿真分析, 验证了算法的有效性.本文内容主要包括建立整星隔振平台模型、系统动力学模型、控制算法设计与仿真结果分析.
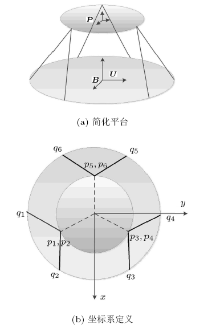
采用Stewart平台, 设计整星隔振平台如图1(a)所示, 平台由六根支杆并联构成, 具有六自由度. 支杆结构如图1(b)所示, 支杆集成了磁流变阻尼器和弹簧, 起到弹性支撑和阻尼作用.
将整星隔振平台简化为如图2(a)所示的模型, 将上平台和基础简化为刚体, 即具有平动和转动共6个自由度, 定义B和P分别为基础固连坐标系和上平台固连坐标系原点, P点选取为上平台质心位置, U为惯性坐标系原点, 为方便矢量运算转为矩阵计算, 选取U, B和P三个坐标系的坐标轴方向相同, 支杆两端的编号与坐标轴方向如图2(b)所示.
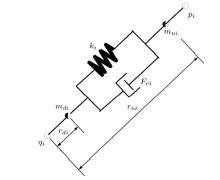
支杆两端采用球铰与上平台和基础相连, 将支杆简化为上部和下部质量, 以及连接上下部质量的弹簧和磁流变阻尼器, 考虑上下两部分转动惯量, 支杆各部分符号定义如图3所示.
文献[15]提出了多杆被动减振平台的建模方法, 在此基础上, 增加磁流变阻尼力, 忽略球铰阻尼和黏性阻尼.
支杆下部对上部的作用力${\pmb F}_{pi} $由弹簧弹力和磁流变阻尼器阻尼力两部分构成, 即
$ {\pmb u}_i \cdot {\pmb F}_{pi} = - k_i (l_i - l_{ri} ) - F_{ci} \quad(1) $
式中, $k_i $为弹簧刚度; $l_i = \left\| {{\pmb w}_i } \right\|$为支杆长度; ${\pmb u}_i = {\pmb w}_i / l_i $为支杆方向单位向量; $F_{ci} $为杆上部对下部磁流变阻尼器阻尼力, 沿${\pmb u}_i $方向为正; $l_{ri} $为支杆静长度. 下标$i$为1$\sim$6的整数, 代表6根支杆.
直接给出平台线性化动力学方程
${\pmb M}_P \ddot{\pmb X}_P + {\pmb K}_P {\pmb X}_P = {\pmb M}_B \ddot{\pmb X}_B +\\ \qquad {\pmb K}_B {\pmb X}_B + {\pmb F}_e + {\pmb W}{\pmb F}_c + {\pmb G} \quad(2) $
式中, ${\pmb X}_P = \left[\!\!\begin{array}{l} {\pmb x}_P \\ \theta _P \end{array}\!\!\right]$, ${\pmb X}_B = \left[\!\!\begin{array}{l} {\pmb x}_B \\ \theta _B \end{array}\!\! \right]$为${P}$系和${B}$系原点相对${ U}$系的位置向量; ${\pmb F}_e \left[\!\!\begin{array}{1} {\pmb f}_e \\ {\pmb M}_e \end{array}\!\! \right]$, ${\pmb f}_e $和${\pmb M}_e $为卫星对上平台的力和力矩; ${\pmb M}_B $为质量阵; ${\pmb K}_P $, ${\pmb K}_B $为刚度阵; ${\pmb F}_c = \left[ {\pmb F}_{c1}\, , \ {\pmb F}_{c2}\, , \ \cdots \, , \ {\pmb F}_{c6} \right]^{\rm T}$为磁流变阻尼力; $ {\pmb G}$为与重力和位置相关的常数阵; ${\pmb W}$为位置矩阵
${\pmb W}= - \left[ \!\!\begin{array}{cccc} {{\pmb u}_1 } & {{\pmb u}_2 } & \cdots & {{\pmb u}_6 } \\ { }^P\tilde {\pmb p}_1 {\pmb u}_1 & { }^P\tilde{\pmb p}_2 {\pmb u}_2 & \cdots & { }^P\tilde{\pmb p}_6 {\pmb u}_6 \end{array}\!\! \right] $
${ }^P\tilde{\pmb p}_i $为${\pmb p}_i $相对${ P}$系坐标${ }^P{\pmb p}_i $的叉乘矩阵.
为建立平台和卫星的动力学模型, 采用固定界面模态综合法[16], 将卫星的缩聚模型和平台动力学模型进行模态综合, 连接界面假设为刚体, 界面共含有一个节点, 6个自由度.
缩聚后, 将卫星的振动方程改写为模态坐标$\bar {\pmb p}_i $和界面物理坐标${\pmb x}_j $表示的形式, 其中界面物理坐标${\pmb x}_j = {\pmb X}_P $. 设模态坐标$\bar{\pmb p}_i $自由度数为$n$.
采用NASTRAN软件建立卫星有限元模型, 选取合适的模态阶数$n$, 利用DMAP语言输出模型的缩聚质量阵与缩聚刚度阵[17]. 卫星的缩聚模型为
$\left[ \!\! \begin{array}{cc} {\pmb I} & {\bar {\pmb m}_{ij} } \\ {\bar{\pmb m}_{ji} } & {\bar {\pmb m}_{jj} } \end{array}\!\! \right]\left[\!\!\begin{array}{c} {\ddot {\bar {\pmb p}}_i } \\ {\ddot {\pmb x}_j } \end{array} \!\! \right] + \left[\!\! \begin{array}{cc} {\bar {\pmb k}_{ii} } & {\bf 0} \\ {\bf 0} & {\bar {\pmb k}_{jj} } \end{array} \!\! \right]\left[\!\! \begin{array}{c} {\bar {\pmb p}_i } \\ {\pmb x}_j \end{array} \!\!\right] =\\ \qquad \left[\!\! \begin{array}{c} {\bf 0}\\ { - {\pmb F}_e } \end{array} \!\! \right] \quad \quad \quad \quad \quad \quad \quad \quad (3)$
将式(2)和式(3)相加, 可以得到平台和卫星的动力学模型
$ \left[ \!\!\begin{array}{cc} \bar {\pmb m}_{jj} + {\pmb M}_{P} & \bar{\pmb m}_{ji} \\ \bar{\pmb m}_{ij} & {\pmb I} \end{array} \!\! \right]\left[\!\!\begin{array}{c} {\ddot {\pmb x}_j } \\ {\ddot {\bar {\pmb p}}_i } \end{array}\!\!\right] +\\ \qquad \left[\!\!\begin{array}{cc} {\bar {\pmb k}_{jj} + {\pmb K}_P } & {\bf 0} \\ {\bf 0} & \bar {\pmb k}_{ii} \end{array}\!\!\right]\left[\!\! \begin{array}{cc} {\pmb x}_j \\ {\bar {\pmb p}_i } \end{array}\!\!\right] =\\ \qquad \left[ \!\! \begin{array}{c} {\pmb M}_B \ddot {\pmb X}_B +{\pmb K}_B {\pmb X}_B + {\pmb W}{\pmb F}_c + {\pmb G} \\ {\bf 0} \end{array}\!\! \right] \quad (4)$
令
${\pmb M}_x \!=\! \left[\!\!\begin{array}{cc} \bar {\pmb m}_{jj} +{\pmb M}_{P} & \bar {\pmb m}_{ji} \\ {\bar {\pmb m}_{ij} } & {\pmb I} \end{array}\!\! \right]$, ${\pmb K}_x \!=\! \left[\!\!\begin{array}{cc} {\bar {\pmb k}_{jj} + {\pmb K}_P } & {\bf 0} \\ {\bf 0} & \bar {\pmb k}_{ii} \end{array} \!\! \right]$
选取状态变量${\pmb X} = \left[ \dot {\pmb X}_P \ \ \dot {\bar {\pmb p}}_i {\pmb X}_P \ \ \bar {\pmb p}_i \right]$, 将式(4)改写为状态空间模型
$\dot{\pmb X} = {\pmb A}{\pmb X} + {\pmb B}{\pmb U} \quad(5)$
式中
$ {\pmb U} \!=\! \left[ {\pmb F}_c \ \ {\ddot{\pmb X}_B } \ \ {{\pmb X}_B } \ \ {\pmb G} \right]^{\rm T} \\ {\pmb A} = \left[ \!\!\begin{array}{cc} {\bf 0} & { - {\pmb M}_x^{ - 1} {\pmb K}_x } \\ {\pmb I} & {\bf 0} \end{array}\!\!\right] \\ {\pmb B} = \left[\!\!\begin{array}{cccc} {\pmb M}_J {\pmb W} & {\pmb M}_J {\pmb M}_B & {\pmb M}_J {\pmb K}_B & {\pmb M}_J \\ {\bf 0} & {\bf 0} & {\bf 0} & {\bf 0} \end{array}\!\!\right] \quad $
其中, ${\pmb M}_J $为矩阵${\pmb M}_x^{ - 1} $的前6列
状态方程中, ${\pmb G}$为常数阵, 确定了状态变量${\pmb X}$的平衡位置, 不影响系统动态特性, 控制系统设计时可以不加以考虑. 有限时长外激励${\pmb X}_B $作为干扰, 实时改变系统状态值, 控制系统设计为最优调节器问题
因此, 控制系统设计时忽略${\pmb G}$和${\pmb X}_B $的影响, 系统状态空间方程为
$\dot{\pmb X} = {\pmb A}{\pmb X }+ {\pmb B}_J {\pmb F}_c \, , \ \ {\pmb B}_J = \left[ \begin{array}{c} {\pmb M}_J {\pmb W} \\ {\bf 0} \end{array} \right] \quad(6) $
对于线性定常无限时间LQR问题, 一般性能指标为
$J = \int_0^\infty ({\pmb X}'{\pmb Q}{\pmb X} + {\pmb F}_c '{\pmb R}{\pmb F}_c) d t \quad(7)$
${\pmb Q}$和${\pmb R}$分别为半正定和正定常数矩阵, 不考虑系统状态 ${\pmb X}$和控制量${\pmb F}_c $在频域的变化特征.针对我国运载火箭星箭界面低频振动环境在特定频段振动量级较大的特点, 需要对特定频段进行重点衰减, 以纵向振动40Hz为例, 采用频域加权方法对上述性能指标进行改进.选取性能指标为
$\left.\begin{array}{l} J = \int_0^\infty (P\ddot {x}_{pz}^2 + {\pmb X}^{\rm T}\bar{\pmb Q}{\pmb X} +{\pmb F}_c^{\rm T}{\pmb R}{\pmb F}_c )d t \\ \bar{\pmb Q} ={\pmb Q}\, , \ \ \bar{\pmb Q}(3, 3) ={\bf 0} \end{array}\right\} \quad(8) $
根据Parsval定理, 将性能指标式(8)转换为频域形式.
$J = \dfrac{1}{2\pi }\int_{ - \infty }^\infty \Big( \ddot {x}_{pz} ({\rm j}\omega ) P({\rm j}\omega )\ddot {x}_{pz} ({\rm j}\omega ) + \\ \qquad {\pmb X}'({\rm j}\omega)\bar{\pmb Q}{\pmb X}({\rm j}\omega) +{\pmb F}'_c ({\rm j}\omega) {\pmb R}{\pmb F}_c ({\rm j}w)\Big) d\omega \quad(9) $
式中, $\bar {\pmb Q}$和${\pmb R}$为常数阵. 令$P({\rm j}\omega ) = W_z ({\rm j}\omega )qW_z ({\rm j}\omega )$, $W_z ({\rm j}\omega )$为加权函数, $q$为常数, ${\rm j}=\sqrt{-1}$.
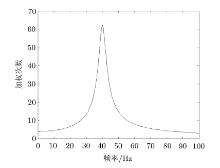
设加权函数$W_z (s) = \dfrac{as + b}{s^2 + cs + d}$, $W_z (s)$ 需满 \vskip 1mm \n 足稳定性条件, 即$c > 0$, $d > 0$. 令$s = {\rm j}\omega $, 设计$W_z ({\rm j}\omega )$的幅频特性如图4所示, 在40Hz处存在峰值, 即增加了性能指标中纵向振动加速度在40Hz处的权值, 以降低40Hz处的振动响应.
为将式(9)重新写为时域形式, 令
$\bar {x}_{pz} (s) = W_z (s)\ddot {x}_{pz} (s) = sW_z (s)\dot {x}_{pz} (s) \quad(10)$
因为$sW_z(s)$的特征方程可能存在共轭复根, 采用文献[12, 13, 14]中的串联分解法会导致系统矩阵中出现复数, 因此采用直接分解法, 将式(10)写为状态空间形式.
$\left[ \!\!\begin{array}{l} \dot {\bar {x}}_1 \\ \dot {\bar {x}}_2 \end{array}\!\!\right] = \left[\!\!\begin{array}{cc} 0 & 1 \\ { - d} & { - c} \end{array}\!\!\right]\left[\!\!\begin{array}{l} \bar {x}_1 \\ \bar {x}_2 \end{array}\!\! \right] + \left[\!\!\begin{array}{l} 0 \\ 1 \end{array}\!\! \right]\dot {x}_{pz} \\ \bar {x}_{pz} = \left[ { - ad} \ \ {b - ac} \right]\left[\!\! \begin{array}{l} \bar {x}_1 \\ \bar {x}_2 \end{array}\!\! \right] + a\dot {x}_{pz} $
令
$\tilde {\pmb A} = \left[\!\!\begin{array}{cc} 0 & 1 \\ { - d} & { - c} \end{array} \!\! \right]\, , \ \ \tilde {\pmb C} = \left[ { - ad} \ \ {b - ac} \right] $
新增系统状态变量$\bar {x}_1 $和$\bar {x}_2 $, 增广状态变量$\bar {\pmb X} = \left[ X \ \ {\bar {x}_1 } \ \ {\bar {x}_2 } \right]^{\rm T}$, 系统状态空间方程为
$\left.\begin{matrix} \dot{\bar{X}}=\bar{A}\bar{X}+\bar{B}F_{c} \\ \bar{Y}=\left[^{X}_{\bar{X}_{pz}}\right]=\bar{C}\bar{X} \\\end{matrix}\right\} (11)$
式中
$ \bar{\pmb A} = \left[\!\!\begin{array}{cc} {\pmb A} & {\bf 0} \\ {\pmb\varDelta}_1 & \tilde{\pmb A} \end{array} \!\! \right]\, , \ \ \bar{\pmb B} = \left[\!\! \begin{array}{c} {\pmb B }\\ {\bf 0} \end{array}\!\! \right]\, , \ \ \bar {\pmb C} = \left[\!\! \begin{array}{cc} {\pmb I } & {\bf 0} \\ {\pmb \varDelta}_2 & \tilde {\pmb C} \end{array} \!\!\right] \\ {\pmb \varDelta}_1 = \left[\!\! \begin{array}{ccccc} 0 & 0 & 0 & 0 & \cdots \\ 0 & 0 & 1 & 0 & \cdots \end{array}\!\! \right]\\ {\pmb \varDelta}_2 = \left[ \!\!\begin{array}{ccccc} 0 & 0 & 1 & 0 & \cdots \end{array}\!\!\right] $
将频域性能指标式(9)改写到时域, 性能指标为
$ J = \int_0^\infty \Big( \bar{\pmb Y}^{\rm T}\hat{\pmb Q}\bar{\pmb Y} + {\pmb F}_c ^{\rm T}{\pmb R}{\pmb F}_c \Big )d t =\\ \qquad \int_0^\infty \Big (\bar {\pmb X}^{\rm T}{\pmb C}^{\rm T}\hat {\pmb Q}\bar {\pmb C}\bar{\pmb X} + {\pmb F}_c ^{\rm T}{\pmb R}{\pmb F}_c \Big) d t \quad(12) $
式中, $\hat {\pmb Q} = \left[\!\! \begin{array}{cc} \bar {\pmb Q} & \\ & q \end{array}\!\!\right]$ .
对于增广系统状态空间方程(11)和加权性能指标(12), 可以设计最优状态调节控制器
${\pmb F}_c = - {\pmb K}\bar {\pmb X}\, , {\pmb K} = - {\pmb R}^{ - 1}\bar{\pmb B}^{\rm T}{\pmb P} $
其中${\pmb P}$是如下Riccati矩阵代数方程的非负定解
${\pmb P}\bar{\pmb A} + \bar{\pmb A}^{\rm T}{\pmb P} - {\pmb P}\bar{\pmb B}{\pmb R}^{ - 1}\bar {\pmb B}^{\rm T}{\pmb P} + \bar{\pmb C}^{\rm T}\hat {\pmb Q}\bar {\pmb C} ={\bf 0} $
频域加权最优控制需要进行全状态反馈, 然而非界面自由度$\bar{\pmb p}_i $是在模态坐标下表示, 不能够完全测量和观测, 因而在实际应用中无法实现, 需要设计部分状态变量进行反馈的次优控制器. 设能够测量和观测的状态变量${\pmb X}_k = {\pmb C}_k \bar{\pmb X}$, 设计反馈矩阵${\pmb K}_k $, 次优控制量${\pmb F}_k = - {\pmb K}_k {\pmb C}_k \bar {\pmb X}$, 然而由于一般${\pmb C}_k $为非可逆阵, 因而一般无法求得${\pmb K}_k $使${\pmb F}_k ={\pmb F}_c $, 可以采用最小范数法$^{[13]}$求得${\pmb K}_k $, 使$\left\| {\pmb K}_k {\pmb C}_k - {\pmb K} \right\|$达到最小.
$\left\| {{\pmb K}_k {\pmb C}_k - {\pmb K}} \right\| = \sqrt {{\pmb T}{\pmb r}({\pmb K}_k {\pmb C}_k - {\pmb K})^{\rm T}({\pmb K}_k {\pmb C}_k - {\pmb K})} $
可以求得${\pmb K}_k = {\pmb K}{\pmb C}_k^{\rm T} ({\pmb C}_k {\pmb C}_k^{\rm T} )^{ - 1}$.
由于磁流变阻尼器的输出力大小不仅与输入电流相关, 还与阻尼器位移和速度相关, 对于次优控制力${\pmb F}_k $, 磁流变阻尼器不能够完全跟踪, 当第$i$个阻尼器期望阻尼力$F_{ki} $与相对速度方向相反且小于最大阻尼力$F_{\max } $时, 通过调节输入电流, 可以实现对期望阻尼力的跟踪, 当$F_{ki} \dot {l}_i \geqslant 0$时, $F_{ki} $与$F_{ci} $方向相反, 则控制输入电流$I = 0$, 为考察外层控制算法的有效性, 故假设内层控制器为理想控制器, 故阻尼器输出力为
$F_{ai} = \left\{ \begin{array}{ll} F_{\max } & (F_{ki} \dot {l}_i < 0, \left| {F_{ki} } \right| \geqslant F_{\max }) \\ F_{ki} & (F_{ki} \dot {l}_i < 0, \left| {F_{ki} } \right| < F_{\max }) \\ {F(I = 0)} & (F_{ki} \dot {l}_i \geqslant 0) \end{array} \right.\\ (i = 1, 2, \cdots, 6) \quad $
在支杆上部安装有加速度传感器, 可以测量$p_i $点沿$u_i $方向加速度$\ddot {\gamma }$, 积分后得到速度$\dot {\gamma }$和位移$\gamma $, 通过雅可比矩阵${\pmb\varGamma} $可以得到${\pmb X}_P ={\pmb \varGamma}^{ - 1}{\pmb\gamma} $
${\pmb\gamma} = \left[ \!\!\begin{array}{c} {\gamma _1 } \\ {\gamma _2 } \\ \vdots \\ {\gamma _6 } \end{array} \!\! \right]\, , \ \ {\pmb\varGamma} = \left[\!\!\begin{array}{cc} {u_1 } & {{ }^P\tilde {p}_1 u_1 } \\ {u_2 } & {{ }^P\tilde {p}_2 u_2 } \\ \vdots & \vdots \\ {u_6 } & {{ }^P\tilde {p}_6 u_6 } \end{array} \!\! \right] $
设状态变量$\bar {x}_1 $和$\bar {x}_2 $的初始值为零, 则$\bar {x}_1 $和$\bar {x}_2 $可以由$\dot {x}_{pz}$确定, 故采用如下两种次优控制策略, 比较控制效果, 控制状态变量选取为
$ {\pmb X}_{k1} = [ \dot{\pmb X}_P \ \ {\pmb X}_P ] \\ {\pmb X}_{k2} = \left[ \dot {\pmb X}_P \ \ {\pmb X}_P \ \ \bar {x}_1 \ \ \bar {x}_2 \right] $
以下平台纵向振动位移$x_{bz} $为输入, 上平台纵向振动位移$x_{pz}$为输出, 考察纵向位移传递率在不同控制作用下的变化情况. 纵向传递率$T(s)$为
$T(s) = \dfrac{x_{pz} (s)}{x_{bz} (s)}$
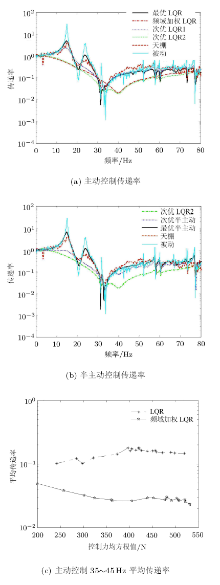
主动控制效果对比如图5(a)所示, 相对被动控制, 频域加权LQR控制、LQR控制与天棚阻尼控制均能显著降低传递率, 天棚阻尼控制与LQR控制效果相当, 天棚阻尼控制在高频段控制效果变差, 频域加权最优控制在40Hz处对传递率具有明显抑制作用, 且在其他频段基本无恶化, 且在大部分频段能显著降低位移传递率.次优控制1的控制效果与最优LQR控制效果相当, 次优控制2的控制效果与频域加权LQR最优控制效果相当, 说明反馈控制变量$\bar{x}_1 $ 和$\bar {x}_2 $起到主要作用.在LQR控制和次优控制2中增加磁流变阻尼器控制器后, 控制效果如图5(b)所示, 相对主动控制, 半主动控制控制减振效果变差, 但是频域加权次优半主动控制在40Hz处依然可以衰减50%的振动, 40Hz处纵向传递率从0.15降至0.07.通过调整权值矩阵中参数, 改变控制作用力均方根值大小, 图5(c)为主动控制作用下, 35Hz$\sim$45Hz平均传递率随控制力均方根值变化曲线, 频域加权LQR最优控制相对传统最优控制在40Hz附近振动具有明显的抑制作用.
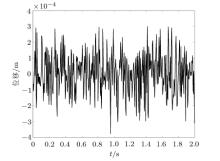
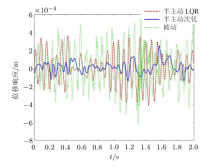
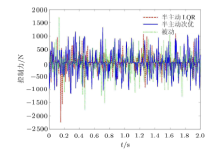
图6$ \sim $图8为时域历程, 输入频率范围为0 $\sim$ 100 Hz的白噪声随机激励$x_{bz}$, 如图6所示, 位移响应$x_{pz} $和控制力如图7和图8所示, 从图7和图8中可以看出, 在控制力均方根值为250N附近时, 半主动次优控制可以明显降低位移幅值, 具有更好的控制效果.
为改善星箭界面力学环境, 设计新型整星隔振平台.通过牛顿-欧拉法建立了隔振平台多体动力学模型, 利用NASTRAN对卫星有限元模型进行模态截断, 采用模态综合法建立系统动力学模型.为解决我国运载火箭星箭界面力学环境在特定频段振动量级较大的问题, 采用频域加权LQR控制算法, 对特定频段振动在性能指标中进行加权, 改进原有串联分解法, 采用直接分解法扩展系统状态变量, 通过测量加速度信号进行反馈控制.以纵向振动为例, 仿真结果表明, 频域加权LQR算法可以有效降低卫星在特定频段传递率, 且在其他频段没有恶化, 具有重要的工程应用价值.
The authors have declared that no competing interests exist.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|