引用本文
张英蓉, 沈火明, 张波. 非局部应变梯度理论下纳米梁的力学特性研究1) . 力学与实践, 2018,40(2): 167-172
ZHANG Yingrong, SHEN Huoming, ZHANG Bo. INVESTIGATIONS ON THE MECHANICAL CHARACTERISTICS OF NANOBEAMS BASED ON THE NONLOCAL STRAIN GRADIENT THEORY1) . MECHANICS IN ENGINEERING, 2018,40(2): 167-172.  
Doi: 10.6052/1000-0879-17-361
Permissions
Copyright©2018, 《力学与实践》编辑部
《力学与实践》编辑部 所有
非局部应变梯度理论下纳米梁的力学特性研究1)
张英蓉, 沈火明2), 张波
西南交通大学力学与工程学院,成都 610031
应用力学与结构安全四川省重点实验室,成都 610031
2) 沈火明,教授. E-mail: hmshen123@126.com
收稿日期: 2017-10-25
资助项目: 1) 国家自然科学基金资助项目(11672252,11602204).
摘要

基于非局部应变梯度理论,建立了一种具有尺度效应的高阶剪切变形纳米梁的力学模型. 其中,考虑了应变场和一阶应变梯度场下的非局部效应. 采用哈密顿原理推导了纳米梁的控制方程和边界条件,并给出了简支边界条件下静弯曲、自由振动和线性屈曲问题的纳维级数解. 数值结果表明,非局部效应对梁的刚度产生软化作用,应变梯度效应对纳米梁的刚度产生硬化作用,梁的刚度整体呈现软化还是硬化效应依赖于非局部参数与材料特征尺度的比值. 梁的厚度与材料特征尺度越接近,非局部应变梯度理论与经典弹性理论所预测结果之间的差异越显著.

关键词: 非局部应变梯度理论; 尺度效应; 高阶剪切变形; 纳米梁
中图分类号:O343.5 文献标志码:A
INVESTIGATIONS ON THE MECHANICAL CHARACTERISTICS OF NANOBEAMS BASED ON THE NONLOCAL STRAIN GRADIENT THEORY1)
ZHANG Yingrong, SHEN Huoming2), ZHANG Bo
School of Mechanics & Engineering, Southwest Jiaotong University, Chengdu 610031, China
Applied Mechanics and Structure Safety Key Laboratory of Sichuan Province, Chengdu 610031, China
Abstract

A size-dependent mechanical model of nanobeam is built within the framework of the nonlocal strain gradient theory. The present model considers the nonlocal effects of the strain field and first gradient strain field, as well as the high-order shear deformation effect. Governing equations and boundary conditions are derived simultaneously by using Hamilton’s principle. The Navier-type solutions are developed for nanobeams with simply-supported boundary conditions. Parametric studies are performed to exhibit the static bending, free vibration and linear buckling behaviors of nanobeams with different groups of geometrical and material parameters. It is found that the non-local effect produces a softening effect on the stiffness of the beam while the strain gradient effect produces a hardening effect, the stiffness of nanobeams is significantly dependent on the ratio between the nonlocal parameter and strain gradient parameter. In addition, the stiffness-hardening or stiffness-softing effects become increasingly significant as the thickness is close to the material characteristic and can be negligible when the thickness is sufficient large.

Key words: nonlocal strain gradient theory; size effect; high-order shear deformation; nanobeam

随着工程结构逐渐向微型化、智能化的方向发展, 纳米梁在微机电系统、生物传感器和原子力显微镜 等领域得到日益广泛的应用[1]. 在研究微尺度结构力学性能的诸多方法中, 实验研究由于对试样、仪器和测试方法的严苛要求, 以及对精度控制的困难性而备受局限. 分子动力学模拟和离散位错动力学模拟也因程序计算量巨大, 计算效率较低而难以进行[2]. 在微纳米尺度下, 材料特征长度尺寸接近材料颗粒尺寸, 结构的尺度效应不可忽略, 传统连续介质理论已无法准确预测微纳米 尺度结构的力学性能[3], 因此, 考虑尺度效应的非局部理论[4], 偶应力理论[5], 应变梯度理论[6]等高 阶理论成为微纳米力学领域的研究重点.

非局部理论认为, 结构内某一点的应力不仅与该点的应变有关, 而且与该点附近区域内所有点的应变有关[7]. 应变梯度理 论则将连续体中的每一个物质点看作含有高阶应变的胞元, 据此引入长度尺度参数来表征其对结构力学性能的影响[8]. Lim等[9]在2015年提出了非局部应变梯度理论, 该理论考虑了非局部效应和应变梯度效应. 基于该理论, Li等[10]分析了尺寸相关杆的轴向振动, 得到了不同边界条件下杆的固有频率解析解. Li等[11]建立了非局部应变梯度非线性欧拉--伯努利纳米梁模型, 并进行了屈曲分析, 获得了简支梁的后屈曲挠度和临界屈曲力. Ebrahimi等[12]探究了热环境下功能梯度纳米梁内的波传播行为, 以及温度、非局部效应、应变梯度效应对波频和相速度的影响. Ebrahimi等[13]还建立了非局部应变梯度理论下的非均匀功能梯度纳米板的波传播模型, 并与经典弹性理论模型做了对比. Sim sek[14]研究了功能梯度纳米梁的非线性振动, 通过新型哈密顿法给出了非线性振动频率的近似解.

本文基于非局部应变梯度理论和Reddy高阶剪切变形理论, 建立了纳米梁的动静力学问题理论模型, 以简支纳米梁为例, 给出 了梁的弯曲、振动和屈曲的纳维级数解, 探讨非局部参数、材料特征长度参数及结构尺寸对纳米梁挠度、固有频率和临界屈曲 力的影响.

1 控制方程建立

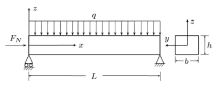
考虑一个两端简支矩形截面Reddy梁, 梁的横截面积为 A, 其余尺寸参数及坐标设置如图1所示, u1, u2, u3分别为纳米梁沿 x, y, z方向的位移

$u_1 = u\left( {x, t} \right) + z\phi \left( {x, t} \right) - \\ \qquad c_1 z^3\left[ {\phi \left( {x, t} \right) + \dfrac{\partial }{\partial x}w\left( {x, t} \right)} \right] \quad (1)$

$u_2 = 0, \; \; \; \; \; u_3 = w(x, t) \quad (2)$

式中 u, ϕ, w分别为梁的平移位移, 转角位移和挠度. 相应的非零应变为

$\varepsilon _{xx} = \dfrac{\partial u}{\partial x} + z\dfrac{\partial \phi }{\partial x} - c_1 z^3\left( {\dfrac{\partial \phi }{\partial x} + \dfrac{\partial ^2w}{\partial x^2}} \right) \quad (3)$

$2\varepsilon _{xz} = \phi - c_2 z^2\left( {\phi + \dfrac{\partial w}{\partial x}} \right) + \dfrac{\partial w}{\partial x} \quad (4)$

其中, c1=4/3h2, c2=4/h2. 在Reddy梁理论下, 无需额外引入剪切修正系数, 且在梁的 上下表面(即 z=±h/2时), 剪应变等于0, 相较于欧拉--伯努利梁和铁木辛柯梁而言更符合实际情况[15].

图1 纳米梁尺寸参数及坐标设置示意图

根据非局部应变梯度理论, 应力可以表示为

tij=σij-∇σij(1)(5)

其中, ∇是拉普拉斯算子, σij和 σij1分别是经典非局部应力和高阶非局部应力

σij=∫V‍α0r-r', eaε'ijr'dV6

σij(1)=l2∫V‍α1r-r', eaε'ij, ir'dV(7)

式中, ε'ij和 ε'ij, i分别为应变和应变梯度. ea是表征非局部效应的长度参数, α0r-r', ea和 α1r-r', ea是非局部核函数, r-r'是弹性体内不同两点间的距离, l是表征高阶应变梯度效应的材料特征长度.

鉴于非局部应变梯度积分本构方程求解困难, 实际计算中, 常使用其微分形式

1-ea2∇2txx=E1-l2∇2εxx(8)

1-ea2∇2txz=2G1-l2∇2εxz(9)

其中, E为材料的弹性模量, G为剪切模量.

当 ea=0时, 式(8) 和式 (9) 退化为应变梯度理论本构方程; 当 l=0时, 退化为非局部弹性理论本构方程.

局部应变梯度理论下的应力和高阶应力沿横截面的内力分别为

$\left.\begin{array}{1} N = \int_A {t_{xx} } d A\, , \ \ M = \int_A {zt_{xx} } d A \\ P = \int_A {z^3t_{xx} } d A\, , \ \ Q = \int_A {t_{ xz} } d A \\ R = \int_A {z^2t_{\rm xz } } d A \end{array} \right\} \quad (10)$

$\left.\begin{array}{1} N^{(1)} = \int_A {\sigma _{ xx }^{(1)} } d A\, , \ \ M^{(1)} = \int_A {z\sigma _{ xx }^{(1)} } d A \\ P^{(1)} = \int_A {z^3 \sigma _{ xx }^{(1)} } d A\, , \ \ Q^{\left( 1 \right)} = \int_A {\sigma _{ xz }^{(1)} } d A \\ R^{(1)} = \int_A {z^2\sigma _{ xz }^{(1)} } d A \end{array} \right\} \quad (11)$

式中, P, R, P(1)和 R(1)只在高阶理论中出现.

纳米梁应变能的变分形式可写为

$\delta U = \int_V {\left( {\sigma _{xx} \delta \varepsilon _{xx} + \sigma _{xx}^{(1)} \nabla \delta \varepsilon _{xx} } \right)} d V +\\ \qquad \int_V {\left( {2\sigma _{xz} \delta \varepsilon _{xz} + 2\sigma _{xz}^{(1)} \nabla \delta \varepsilon _{xz} } \right)} d V \quad(12) $

动能的变分形式为

$\delta T = \int_0^L {\rho A\left( {\dfrac{\partial u_1 }{\partial t}\dfrac{\partial \delta u_1 }{\partial t} + \dfrac{\partial u_2 }{\partial t}\dfrac{\partial \delta u_2 }{\partial t} + \dfrac{\partial u_3 }{\partial t}\dfrac{\partial \delta u_3 }{\partial t}} \right)} d x \quad(13) $

考虑轴向压力 FN和横向均布力 q所做外力功, 其变分形式为

$\delta W = \int_0^L {\left( {q\delta w + F_N \dfrac{ d w}{d x}\dfrac{d\delta w}{d x}} \right)} d x \quad (14)$

根据哈密顿原理

∫t1t2‍δT-δU+δWdt=0(15)

将式(12) ~式(14)分别代入式(15)中进行分部积分, 由变分基本引理提取 δu, δw和 δϕ项相关系数可得到梁的运动方程

$\delta u: - \dfrac{\partial N}{\partial x} = m_0 \dfrac{\partial ^2{ u}}{\partial t^2} \quad (16)$

$ \delta w: - c_1 \dfrac{\partial ^2P}{\partial x^2} - \dfrac{\partial Q}{\partial x} + c_2 \dfrac{\partial R}{\partial x} + q - \dfrac{\partial }{\partial x}\left( {F_N \dfrac{\partial w}{\partial x}} \right)=\\ \qquad - m_0 \dfrac{\partial ^2w}{\partial t^2} - c_1 m_4 \dfrac{\partial ^3\phi }{\partial x\partial t^2}+\\ \qquad c_1^2 m_6 \left( {\dfrac{\partial ^3\phi }{\partial x\partial t^2} + \dfrac{\partial ^4w}{\partial x^2\partial t^2}} \right) \quad (17)$

$ \delta \phi : - \dfrac{\partial M}{\partial x} + c_1 \dfrac{\partial P}{\partial x} + Q - c_2 R =\\ \qquad - m_2 \dfrac{\partial ^2\phi }{\partial t^2} + c_1 m_4 \left( {2\dfrac{\partial ^2\phi }{\partial t^2} + \dfrac{\partial ^3w}{\partial x\partial t^2}} \right) -\\ \qquad c_1^2 m_6 \left( {\dfrac{\partial ^2\phi }{\partial t^2} + \dfrac{\partial ^3w}{\partial x\partial t^2}} \right) \quad (18)$

其中

m0, m2, m4, m6T=∫A‍ρ1, z2, z4, z6TdA(19)

同时, 根据积分边界项, 可得在 x=0和 x=L处的边界条件为

$N = 0 \ \ \hbox{或} \ \ u = 0 \quad (20a) \\ c_1 \dfrac{\partial P}{\partial x} + Q - c_2 R = 0 \ \ \hbox{或} \ \ w = 0 \quad (20b) \\ M - c_1 P + Q^{(1)} - c_2 R^{(1)} = 0 \ \ \hbox{或} \ \ \phi = 0 \quad (20c) \\ N^{(1)} = 0 \ \ \hbox{或} \ \ \dfrac{\partial u}{\partial x} = 0 \quad (20d) \\ - c_1 P - c_2 R^{(1)} + Q^{(1)} = 0 \ \ \hbox{或} \ \ \dfrac{\partial w}{\partial x} = 0 \quad (20e) \\ M^{(1)} - c_1 P^{(1)} = 0 \ \ \hbox{或} \ \ \dfrac{\partial \phi }{\partial x} = 0 \quad (20f) \\ c_1 P^{(1)} = 0 \ \ \hbox{或} \ \ \dfrac{\partial ^2w}{\partial x^2} = 0 \quad (20g)$

控制方程(16)与经典理论下相同, 对式(8)、式(9)进行积分和变换, 可以将式(17)和式(18)转化为位移形式

$ \left( {1 - l^2\dfrac{\partial ^2}{\partial x^2}} \right)\left[ {c_1 EJ\dfrac{\partial ^3\phi }{\partial x^3} - c_1^2 EK\left( {\dfrac{\partial ^3\phi }{\partial x^3} + \dfrac{\partial ^4w}{\partial x^4}} \right)} \right. +\\ \qquad \left. {G\hat {A}\left( {\dfrac{\partial \phi }{\partial x} + \dfrac{\partial ^2w}{\partial x^2}} \right)} \right] - \left( {1 - \mu ^2\dfrac{\partial ^2}{\partial x^2}} \right) \cdot \\ \qquad \left[ {\dfrac{\partial }{\partial x}\left( {F_N \dfrac{\partial w}{\partial x}} \right) - q} \right] =\\ \qquad \left( {1 - \mu ^2\dfrac{\partial ^2}{\partial x^2}} \right)\left[ {m_0 \dfrac{\partial ^2w}{\partial t^2} + c_1 m_4 \dfrac{\partial ^3\phi }{\partial x\partial t^2}} \right. -\\ \qquad \left. { c_1 ^2m_6 \left( {\dfrac{\partial ^3\phi }{\partial x\partial t^2} + \dfrac{\partial ^4w}{\partial x^2\partial t^2}} \right)} \right] \quad (21)$

$\left( {1 - l^2\dfrac{\partial ^2}{\partial x^2}} \right)\left[ {EI\dfrac{\partial ^2\phi }{\partial x^2} - c_1 EJ\left( {2\dfrac{\partial ^2\phi }{\partial x^2} + \dfrac{\partial ^3w}{\partial x^3}} \right)} \right.+\\ \qquad \left. { c_1^2 EK\left( {\dfrac{\partial ^2\phi }{\partial x^2} + \dfrac{\partial ^3w}{\partial x^3}} \right) - G\hat {A}\left( {\phi + \dfrac{\partial w}{\partial x}} \right)} \right] =\\ \qquad \left( {1 - \mu ^2\dfrac{\partial ^2}{\partial x^2}} \right)\left[ {\bar {m}_2 \dfrac{\partial ^2\phi }{\partial t^2} - c_1 \bar {m}_4 \left( {\dfrac{\partial ^2\phi }{\partial t^2} + \dfrac{\partial ^3w}{\partial x\partial t^2}} \right)} \right] \quad (22)$

其中

A, I, J, KT=∫A‍1, z2, z4, z6TdA(23)

为方便起见, 引入以下参数来简化方程

$\left.\begin{array}{1} {m}_2 = m_2 - c_1 m_4 \, , \ \ \bar {m}_4 = m_4 - c_1 m_6 \\ \bar {I} = I - c_1 J\, , \ \ \bar {J} = J - c_1 K \\ \tilde {A} = A - c_2 I\, , \ \ \tilde {I} = I - c_2 J\, , \ \ \hat {A} = \tilde {A} - c_2 \; \tilde {I} \end{array} \right\} \quad(24) $

2 弯曲、振动及屈曲求解

对于简支梁, 其挠度, 转角和分布载荷可以展开为傅里叶级数

$\left.\begin{array} w(x, t) = \sum_{n = 1}^\infty {W_n \sin \dfrac{n\pi x}{L} {\rm e}^{{\rm i}\omega _n t}} \\ \phi (x, t) = \sum_{n = 1}^\infty {\varPhi _n \cos \dfrac{n\pi x}{L}{\rm e}^{{\rm i}\omega _n t}} \end{array} \right\} \quad (25)$

$\left.\begin{array}{1} q\left( x \right) = \sum_{n = 1}^\infty {Q_n \sin \dfrac{n\pi x}{L}} \\ Q_n = \dfrac{2}{L}\int_0^l {q\left( x \right)\sin } \dfrac{n\pi x}{L} d x \end{array} \right\} \quad (26)$

其中, Wn和 Φn为傅里叶系数, Qn是载荷幅值, ωn是固有频率. 显然, 式 (25) 满足梁的边界条件.

将式(25)和式(26)代入式(21)和式(22)可得

lnc1EJα3Φn-AnαΦn+αWn+

μn[Q+FNα2Wn+m0Wn-c1m4αΦn+

c12m6α(Φn+αWn)]ωn2=0(27)

ln-EI̅α2Φn-BnΦn+αWn+

μnm̅2Φn-c1m̅4α2Φn+αWnωn2=0(28)

$\left.\begin{array}{1} A_n = G\hat {A} + c_1 ^2\alpha ^2EK\, , \ \ B_n = G\hat {A} - c_1 \alpha ^2E\bar {J} \\ \mu _n = 1 + \mu ^2\left( {\dfrac{n\pi }{L}} \right)^2\, , \ \ l_n = 1 + l^2\left( {\dfrac{n\pi }{L}} \right)^2 \\ \alpha = \dfrac{n\pi }{L} \end{array} \right\} \quad (29)$

对于纳米梁的静弯曲问题, 挠度和转角与轴向力、频率及时间相关项无关, 令式(27)和式(28)中 FN, ωn和所有关于时间的求导项为0, 可以得到

$ \left.\begin{array}{1} w(x, t) = \sum_{n = 1}^\infty {\lambda _n } \dfrac{\left( {E\bar {I}\alpha ^2 + B_n } \right)Q\mu _n }{E\alpha ^4l_n \left( {A_n \bar {I} + B_n Jc_1 } \right)}\sin \dfrac{n\pi x}{L} \\ \phi (x, t) = - \sum_{n = 1}^\infty {\dfrac{B_n Q\mu _n }{E\alpha ^3l_n \left( {A_n \bar {I} + B_n Jc_1 } \right)}\cos \dfrac{n\pi x}{L}} \end{array} \right\} \quad(30) $

对于自由振动问题, 高阶惯性项对频率影响较小, 不予考虑(即令 m2=m4=m6=0), 并令式(27)和式(28)中 Qn和 FN等于0, 可以得到纳米梁的固有频率

$\omega _n ^2 = \alpha ^4\dfrac{\left( {A_n E\bar {I} + EJc_1 B_n } \right)\; l_n }{\mu _n {\mkern 1mu} m_0 \left( {\alpha ^2E\bar {I} + B_n } \right)} \quad(31) $

对于屈曲问题, 令式(27)和式(28)中 Qn, ωn和所有关于时间的求导项等于0, 并设 n=1, 可以得到纳米梁的临界屈曲力

$F_{N{\rm cr}} = \dfrac{1}{\mu _1}\dfrac{\pi ^2El_1}{L^2}\dfrac{A_1 \bar {I} + c_1 B_1 J}{E\bar {I}\left( {\pi }/{L}\right)^2 + B_1 }\quad(32) $

3 数值算例及分析

为了探究非局部应变梯度理论下的剪切变形梁模型特点, 采用如下几何和材料参数： L=20h, b=2h, E=30×106MPa, ν=0.3, ρ=1kg/m 2, q=1N/m, 并对相关变量做无量纲化处理

$\bar {w} = - \dfrac{100wEI}{q_0 L^4}\, , \ \ \bar {\omega } = \omega _1 L^2\sqrt {\dfrac{m_0 }{EI}} \, , \ \ \bar {F}_N = \dfrac{F_{N{\rm cr}} L^2}{EI} \quad(33) $

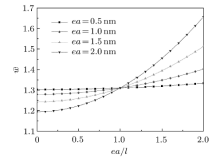
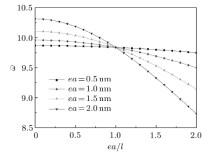
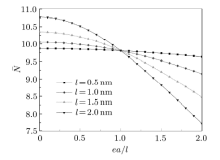
为满足精度要求, 取傅里叶级数前100项, 分别研究非局部参数和材料特征长度的比值对纳米梁弯曲、振动和屈曲 的影响, 如图2 ~图4所示.

图2 非局部参数与材料特征长度的比值对挠度的影响

图3 非局部参数与材料特征长度的比值对固有频率的影响

图4 非局部参数与材料特征长度的比值对临界屈曲力的影响

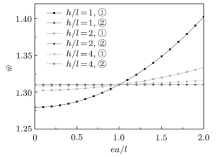
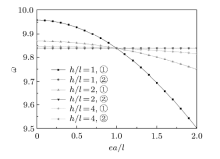
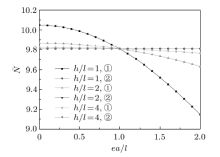
纳米梁刚度总体随非局部长度参数的增加而降低, 随特征长度参数的增加而增强. 但当 ea/l< 1时, 最大弯曲挠度随材料特征长度的增大而减小, 固有频率和临界屈曲力随材料特征长度的增大而增大; 当 ea/l> 1时, 最大弯曲挠度随材料特征长度的增大而增大, 固有频率和临界屈曲力随材料特征长度的增大而减小; 当 ea/l=1时, 纳米梁挠度、固有频率和临界屈曲力值保持不变. 当 l=0时, 所得结果与非局部理论下结果一致[16], 当 ea=0时, 与应变梯度理论下结果相同[17].

取不同尺寸纳米梁, 分别计算经典弹性理论(图中②)和非局部应变梯度理论(图中①)下的挠度、固有频率和临界屈曲力, 如图5 ~图7所示

在非局部应变梯度理论中, 当 ea/l< 1时, 纳米梁挠度与经典弹性理论值相比偏小, 固有频率和临界屈曲力偏大; 当 ea/l> 1时, 纳米梁挠度与经典弹性理论值相比偏大, 固有频率和临界屈曲力偏小; 当 ea/l=1时, 两种理论下所得结果相同. 随着纳米梁高度与材料特征尺度越接近, 结构尺度效应越明显, 非局部应变梯度理论下结果与经典弹性理论结果相比偏差越大, 该现象与实验结果相符[18]. 而在经典弹性理论中, 纳米梁尺寸的等比例变化对无量纲的挠度、固有频率和临界屈曲力没有影响, 纳米结构的尺度效应在经典 弹性理论中无法得以体现.

图5 两种理论下结构尺寸对挠度的影响
(①为非局部应变梯度理论, ②为经典弹性理论)

图6 两种理论下结构尺寸对固有频率的影响
(①为非局部应变梯度理论, ②为经典弹性理论)

图7 两种理论下结构尺寸对临界屈曲力的影响
(①为非局部应变梯度理论, ②为经典弹性理论)

4 结 论

本文从非局部应变梯度理论本构关系出发, 建立了能同时反映剪切变形效应和尺度效应的Reddy梁模型, 并通过哈密顿原理得到了梁的控制方程和边界条件, 求得纳米梁最大弯曲挠度、固有频率和临界屈曲力的解析解, 结合数值算例分析发现：

(1)非局部效应的引入对纳米梁起刚度软化作用, 而应变梯度效应的引入对纳米梁起刚度硬化作用.

(2)当非局部参数大于材料特征长度( ea> l)时, 结构呈现刚度软化效应; 当非局部参数小于材料特征长度( ea< l)时, 结构呈现刚度硬化效应; 当其相等( ea=l)时, 硬化效应和软化效应相互抵消, 挠度、固有频率和临界屈曲力值保持不变并与经典弹性理论下的值相等.

(3)纳米梁高度与材料特征尺度越接近, 非局部应变梯度理论下结果与经典弹性理论结果相比偏差越大.

The authors have declared that no competing interests exist.

参考文献
1 高世桥, 刘海鹏. 微机电系统力学(第1版). 北京: 国防工业出版社, 2008 [本文引用:1]
2 尹春松, 杨洋. 基于非局部铁木辛柯梁模型的碳纳米管弯曲特性研究. 固体力学学报, 2015 (S1): 165-169 [本文引用:1]
3 尹莉. 微尺度下结构的静动力学行为研究. [博士论文]. 武汉: 华中科技大学, 2010 [本文引用:1]
4 Eringen AC. Nonlocal Continuum Field Theories. New York: Springer Science & Business Media, 2002 [本文引用:1]
5 Yang F, Chong ACM, Lam DCC, et al. Couple stress based strain gradient theory for elasticity. International Journal of Solids and Structures, 2002, 39(10): 2731-2743 [本文引用:1]
6 Mindlin RD. Micro-structure in linear elasticity. Archive for Rational Mechanics and Analysis, 1964, 16(1): 51-78 [本文引用:1]
7 Reddy JN, Pang SD. Nonlocal continuum theories of beams for the analysis of carbon nanotubes. Journal of Applied Physics, 2008, 103(2): 023511 [本文引用:1]
8 Kong S, Zhou S, Nie Z, et al. Static and dynamic analysis of micro beams based on strain gradient elasticity theory. International Journal of Engineering Science, 2009, 47(4): 487-498 [本文引用:1]
9 Lim CW, Zhang G, Reddy JN. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. Journal of the Mechanics and Physics of Solids, 2015, 78: 298-313 [本文引用:1]
10 Li L, Hu Y, Li X. Longitudinal vibration of size-dependent rods via nonlocal strain gradient theory. International Journal of Mechanical Sciences, 2016, 115: 135-144 [本文引用:1]
11 Li L, Hu Y. Buckling analysis of size-dependent nonlinear beams based on a nonlocal strain gradient theory. International Journal of Engineering Science, 2015, 97: 84-94 [本文引用:1]
12 Ebrahimi F, Barati MR. Wave propagation analysis of quasi-3D FG nanobeams in thermal environment based on nonlocal strain gradient theory. Applied Physics A, 2016, 122(9): 843 [本文引用:1]
13 Ebrahimi F, Barati MR, Dabbagh A. A nonlocal strain gradient theory for wave propagation analysis in temperature-dependent inhomogeneous nanoplates. International Journal of Engineering Science, 2016, 107: 169-182 [本文引用:1]
14 Simsek M. Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel Hamiltonian approach. International Journal of Engineering Science, 2016, 105: 12-27 [本文引用:1]
15 Zhang B, He Y, Liu D, et al. Size-dependent functionally graded beam model based on an improved third-order shear deformation theory. European Journal of Mechanics-A/Solids, 2014, 47: 211-230 [本文引用:1]
16 Reddy JN. Nonlocal theories for bending, buckling and vibration of beams. International Journal of Engineering Science, 2007, 45(2): 288-307 [本文引用:1]
17 Thai HT. A nonlocal beam theory for bending, buckling, and vibration of nanobeams. International Journal of Engineering Science, 2012, 52: 56-64 [本文引用:1]
18 Kong S, Zhou S, Nie Z, et al. The size-dependent natural frequency of Bernoulli-Euler micro-beams. International Journal of Engineering Science, 2008, 46(5): 427-437 [本文引用:1]