诸多黏性土渗流试验表明,在低水力梯度下渗流会出现明显偏离Darcy定律的现象. 为了分析渗流的非Darcy特性对固结过程 的影响,引入Hansbo渗流方程描述圆柱土样内的渗流,重新推导轴对称条件下的Biot固结方程,并给出方程的Crank--Nicolson有限 差分格式. 通过与Darcy渗流条件下轴对称Biot固结方程解析解的对比,验证计算方法的有效性. 然后分析Hansbo模型参数对圆柱 土样固结过程的影响. 计算结果表明:与Darcy渗流相比,Hansbo渗流会延缓圆柱土样的固结过程. 随着Hansbo渗 流参数
Some clay permeability tests show that the flow of the pore water in clays may depart from the Darcy law under the condition of the lower hydraulic gradient. In order to investigate the influence of the non-Darcy behavior of flow on the consolidation process, the Hansbo equation is introduced to describe the flow in cylindrical soil samples and the Biot consolidation equation under axisymmetric conditions is modified. The numerical analysis is performed by using the Crank--Nicolson finite difference method. The proposed method is validated by comparing the analytical solution of the axisymmetric Biot’s consolidation equation with the Darcy flow. Then the influence of the Hansbo’s flow parameters on the consolidation process of the cylindrical soil sample is investigated. The numerical results show that the Hansbo’s flow delays the consolidation process of the saturated clay compared with the Darcy flow. At the early stage of consolidation, the Mandel--Cryer effect becomes more significant with the increase of the Hansbo’s flow parameters. In other words, the peak value of the pore water pressure will increase, and the reaching of its peak will also be delayed. Similarly, the delaying phenomenon of the pore water pressure dissipation is also more obvious in the later stage of consolidation. However, the Hansbo’s flow has little effect on the displacement in the cylindrical soil.
经典Terzaghi 固结理论奠定了现代土力学的基础, 但由于该理论认为土体中各点的体积应力不随时间而变, 所以在理论上是不严格的. Biot[1]直接从平衡方程, 几何方程和本构方程入手, 使位移与渗流直接耦合, 准确反映出孔隙水压力(孔压)变化与土骨架变形 的相互关系, 使固结理论趋于完善. 在用Biot理论分析饱和黏性土固结问题时, 在固结初期往往会出现孔压不消散反而增大并超过初始孔隙压力的现象[2, 3], 称之为Mandel--Cryer效应. 并且, Gibson等[4]的土球试验证明了这种效应的存在. 后来有不少学者从多方面对该现象进行了分析, 例如, 殷宗泽[5]、纪多辙等[6]、原新生等[7]分别采用有限元法或引入数学级数、Green函数对圆柱土样Biot固结方程进行求解, 分析了材料常数等对该现象的影响. 这些传统的Biot固结理论都假定土体中的渗流符合Darcy定律, 而后者对饱和黏性土的适用性一直受到质疑. Terzaghi早在1925年就指出塑性大的黏土会出现其渗流偏离Darcy定律的现象. 这一论断也得到越来越多渗流试验的证实, 并提出了不同的非Darcy渗流形式[8, 9, 10, 11, 12, 13], 其中应用较为广泛的 当属Hansbo公式[9]
$v = \left\{ \begin{array}{ll} ci^m\, , & i \leqslant i_1 \\ k(i - i_0 ) \, , & i > i_1 \end{array} \right. \quad(1) $
式中,
目前考虑非Darcy特性对固结性状影响的研究大多在一维固结方面. 例如, 谢海澜等[14], 刘忠玉等[15], 鄂建等[16]先后引入Hansbo渗流方程(1)或其简化形式修正Terzaghi固结理论, 参数分析表明, Hansbo渗流会大大延 缓孔压的消散速度. 在此基础上, 其他学者[17, 18, 19, 20, 21]先后又考虑了土体变形非线性及流变特性的影响. Hansbo[22]、周琦等[23]、刘忠玉等[24]则进一步将式(1)或其简化形式引入到砂井地基固结分析中, 但他们并没有考虑孔压与土体变形的耦合效应, 因而仍属 于Terzaghi固结理论. Teh等[25]、邓岳保等[26]和Deng等[27]分别以轴对称或三维Biot固结理论为基础, 分析了Hansbo渗流条件下砂井固结 地基固结度的变化规律, 但并没有讨论其对Mandel--Cryer效应的影响.
为进一步深入讨论渗流模式对饱和黏性土固结特性以及孔压变化规律的影响, 本文拟以圆柱土样为研究对象, 引入方程(1)描述 固结过程中的非Darcy渗流, 修正Biot轴对称固结方程, 并引入有限差分法求其数值解, 进而分析Hansbo渗流参数对固结过程的影响.
本文假定土中渗流服从Hansbo渗流方程(1), 且其中参数在固结过程中为常数, 其余都与Biot固结理论的基本假定相同.为便于应用, 这里将式(1)改写为类似Darcy渗流的形式, 即
$v = {K}'i = - \dfrac{{K}'}{\gamma _{\rm w} }\dfrac{\partial p}{\partial r} =- K\dfrac{\partial p}{\partial r} \quad (2)$
式中,
$K = \dfrac{{K}'}{\gamma _{\rm w} } = \left\{ \begin{array}{ll} k | i | ^{m - 1} / (\gamma _{\rm w} mi_1^{m - 1} ) & (| i | \leqslant i_1 )\\ k [1 - i_1 (m - 1) / ( m | i|)]/ \gamma _{\rm w} & ( | i | > i_1 ) \end{array} \right. $
设线弹性饱和圆柱土样均匀且各向同性, 其半径为
$\dfrac{\partial ^2u}{\partial r^2} + \dfrac{1}{r}\dfrac{\partial u}{\partial r}- \dfrac{1}{r^2}u - \dfrac{(1 + \mu )(1 - 2\mu )}{E(1 - \mu )}\dfrac{\partial p}{\partial r} = 0 \quad (3)$
式中,
半径
$\theta = - ( {\frac{\partial u}{\partial r} + \frac{u}{r}}) \quad (4)$
$ \frac{\partial \theta }{\partial t} = - \frac{1}{r}\frac{\partial }{\partial r}( {r\frac{\partial u}{\partial t}}) \quad (5)$
根据土体渗流连续性条件可得
$\dfrac{\partial \theta }{\partial t} = \dfrac{\partial v}{\partial r} +\dfrac{v}{r} = \dfrac{1}{r}\dfrac{\partial (rv)}{\partial r} \quad (6)$
将式(2)代入式(6)可得
$\dfrac{\partial \theta }{\partial t} = - \dfrac{1}{r}\dfrac{\partial }{\partial r}\left( {rK\dfrac{\partial p}{\partial r}} \right) \quad (7)$
对比式(5)与式(7)可得
$\dfrac{\partial p}{\partial r} = \dfrac{1}{K}\dfrac{\partial u}{\partial t} \quad (8)$
将式(8)代入式(3) 可得以位移表示的平衡方程为
$r^2\dfrac{\partial u}{\partial t} = K_1 \left( {r^2\dfrac{\partial ^2u}{\partial r^2} + r\dfrac{\partial u}{\partial r} - u} \right) \quad (9)$
式中,
方程(8)和方程(9)的边界条件及初始条件为
$- \frac{C_{\rm v} \gamma _{\rm w} }{k(1 - \mu)}[(1 - \mu) \frac{\partial u}{\partial r} + \mu \frac{u}{r}] |_{r = a} = q \quad (10)$
$u(0, t)=0, u(r, 0)=0 \quad (11)$
$p(0, t)< \infty , p(a, t)=0 \quad (12)$
式中,
为了方便数据处理与分析, 引入无量纲参数
$\left.\begin{array}{1} R = \dfrac{r}{a} \, , \ \ U = \dfrac{u}{a} \, , \ \ T = \dfrac{C_{\rm v} t}{a^2} \\ I = \dfrac{i\gamma _{\rm w} a}{q} \, , \ \ I_1 = \dfrac{i_1 \gamma _{\rm w} a}{q} \, , \ \ P = \dfrac{p}{q} \end{array}\right\} \quad(13) $
则式(8)
$\frac{\partial P}{\partial R} = \frac{E(1 - \mu)}{\psi q(1 + \mu)(1 - 2\mu)}\frac{\partial U}{\partial T}\quad (14)$
$R^2\frac{\partial U}{\partial T} = \psi ( R^2\frac{\partial ^2U}{\partial R^2} + R\frac{\partial U}{\partial R} - U) \quad (15)$
$\frac{\gamma _{\rm w} C_{\rm v} }{qk}\frac{\partial U}{\partial R} |_{R = 1} + \frac{\gamma _{\rm w} C_{\rm v} \mu }{k(1 - \mu)}\frac{U}{R} |_{R = 1} = - 1 \quad (16)$
$U(0, T) = 0, U(R, 0) = 0 \quad (17)$
$P(0, T)< \infty, P(1, T)=0 \quad (18)$
式中, 系数$\psi = \left\{ \begin{array}{ll} \left| I \right|^{m - 1} / (mI_1^{m - 1} ) & (\left| I \right| \leq I_1 ) \\ 1 - I_1 (m - 1) / (m\left| I \right|) & (\left| I \right| > I_1 ) \end{array} \right.$.
采用Crank--Nicolson有限差分法求数值解. 在
$A_j U_{j - 1}^{b + 1} + B_j U_j^{b + 1} + C_j U_{j + 1}^{b + 1} = - A_j U_{j -1}^b + D_j U_j^b - C_j U_{j + 1}^b \quad (19) $
式中, 下标
$ A_j = \dfrac{j^2\psi \Delta T}{2} - \dfrac{j\psi \Delta T}{4} \\ B_j = - \left( {j \Delta R} \right)^2 - j^2\psi \Delta T - \dfrac{\psi \Delta T}{2} \\ C_j = \dfrac{j^2\psi \Delta T}{2} + \dfrac{j\psi \Delta T}{4} \\ D_j = - \left( {j \Delta R} \right)^2 + j^2\psi \Delta T + \dfrac{\psi \Delta T}{2} $
边界条件式(16), 式(17)可表示为
$(A_N + C_N )U_{N - 1}^{b + 1} + (B_N - W C_N )U_N^{b + 1} =\\ \qquad -(A_N + C_N )U_{N - 1}^b + (D_N + W C_N )U_N^b + Q C_N \quad(20)$
$U_j^0 = 0 (j =0, 1, 2, \cdots, N) \quad (21)$
$U_0^b = 0 (b =1, 2, \cdots ) \quad (22)$
式中, $W = \dfrac{2a\mu }{N\left( {1 - \mu } \right)}$, $Q = \dfrac{4q\Delta R(1 + \mu )(1 -2\mu )}{E(1 - \mu )}$.
由式(19)
$P_{j - 1}^{b + 1} = P_j^{b + 1} - \dfrac{E\left( {1 - \mu } \right)}{\psi q\left( {1 + \mu } \right)\left( {1 - 2\mu } \right)}\dfrac{U_j^{b + 1} - U_j^b }{\Delta T}\Delta R \quad (23)$
相应的边界条件式(18)可变为
$P_0^b < \infty \, , \quad P_N^b = 0 \quad(24)$
为分析土柱中孔压的整体消散规律, 引入按孔压定义的平均固结度
$U_R = 1 - \dfrac{\int_0^1 {2\pi RPdR} }{\int_0^1 {2\pi RP_0 d R} } = 1 - 2\sum_{j = 0}^{N - 1} {\int_{R_j }^{R_{j + 1} } {RPd R} } \quad(25) $
式中, 时刻
假设孔压
$U_R^b = 1 - 2\sum_{j = 0}^{N - 1} {S_j^b } \quad(26)$
式中
$\begin{array}{l} S_j^b = (P_j^b R_{j + 1} - P_{j + 1}^b R_j )(R_{j + 1}^2 - R_j^2 ) / (2\Delta R)+ \\ \qquad (P_{j + 1}^b - P_j^b )(R_{j + 1}^3 - R_j^3 ) / (3\Delta R) \end{array} $
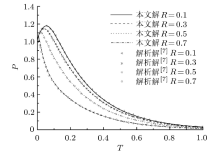
当参数
原新生等[7]已讨论过弹性材料常数等对圆柱土样Biot固结过程的影响, 因此, 这里仅讨论Hansbo渗流参数的影响. 计算中取
为了探讨Hansbo参数对孔压消散的影响, 图2给出了不同Hansbo渗流参数时
图2还表明, 当达到孔压峰值后, 即在固结中后期, 孔压都随时间而逐渐消散, 但在同一时刻
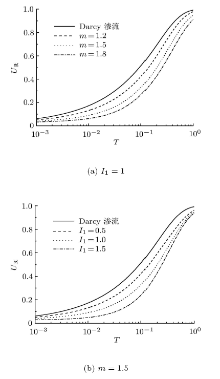
按孔压定义的平均固结度
记
引入Hansbo渗流模型描述饱和黏性土中的非Darcy渗流, 基于Biot固结理论推导了圆柱土样固结方程, 并给出 了方程的Crank--Nicolson有限差分格式. 通过数值分析Hansbo渗流参数
(1) Hansbo渗流参数
(2) Hansbo渗流会延缓圆柱土样内孔压的整体消散, 且
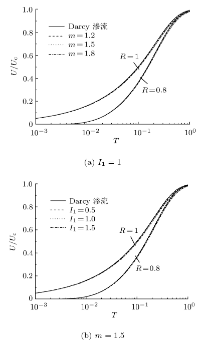
(3)Hansbo渗流对圆柱土样内径向位移的影响不大.
The authors have declared that no competing interests exist.
| 1 |
|
| 2 |
|
| 3 |
|
| 4 |
|
| 5 |
|
| 6 |
|
| 7 |
|
| 8 |
|
| 9 |
|
| 10 |
|
| 11 |
|
| 12 |
|
| 13 |
|
| 14 |
|
| 15 |
|
| 16 |
|
| 17 |
|
| 18 |
|
| 19 |
|
| 20 |
|
| 21 |
|
| 22 |
|
| 23 |
|
| 24 |
|
| 25 |
|
| 26 |
|
| 27 |
|