引用本文
刘彤, 袁勇. 地铁车站增量动力分析的极限状态判定方法1) . 力学与实践, 2018,40(2): 148-154
LIU Tong, YUAN Yong. LIMIT STATE DETERMINATION FOR A SUBWAY STATION STRUCTURE BY INCREMENTAL DYNAMIC ANALYSIS1) . MECHANICS IN ENGINEERING, 2018,40(2): 148-154.  
Doi: 10.6052/1000-0879-17-333
Permissions
Copyright©2018, 《力学与实践》编辑部
《力学与实践》编辑部 所有
地铁车站增量动力分析的极限状态判定方法1)
刘彤*,2), 袁勇*,†,3)
*同济大学地下建筑与工程系,上海 200092
†同济大学土木工程防灾国家重点实验室,上海 200092
2) 刘彤,博士研究生,主要从事地下结构抗震性能研究. E-mail: 262liut@tongji.edu.cn; 3) 袁勇,教授,主要从事地下结构抗震和防灾减灾研究. E-mail: yuany@tongji.edu.cn
收稿日期: 2017-09-25
资助项目: 1)国家自然科学基金 (51208296, 51478343)、上海市科学技术委员会(13231200503)和中央高校基本科研业务费专项资金 (2013KJ095, 101201438)资助项目.
摘要

表征地下结构抗震性能的研究不多,而性能化设计方法需要确定结构物在地震作用下的极限状态. 本文根据地铁车站特点,从结构变形性能和止水性能两个方面定义了抗震性能的四个极限状态,并以结构最大层间位移角 作为特征指标. 以上海某多层地铁车站为背景,建立了土--结构二维有限元模型,采用增量动力分析法 研究该类结构的抗震极限状态,建立了增量动力分析法的地震动强度指标结构底部峰值加速度与结构性能指标最大层间位移角 的关系曲线,给出了该地铁车站结构4个极限状态的最大层间位移角界限值.

关键词: 地铁车站; 性能化设计; 极限状态; 增量动力分析; 性能指标
中图分类号:TU311 文献标志码:A
LIMIT STATE DETERMINATION FOR A SUBWAY STATION STRUCTURE BY INCREMENTAL DYNAMIC ANALYSIS1)
LIU Tong*,2), YUAN Yong*,†,3)
*Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China
†State Laboratory of Disaster Reduction of Civil Engineering, Tongji University, Shanghai 200092, China
Abstract

The seismic performance of the underground structures, is not well studied, while on the other hand, the seismic limit state determination is important for a performance-based design. In this paper, four limit states are defined in terms of the deformation and the waterproof performance of the structure while the maximum story drift angle (θmax) is selected as the characteristic indicator according to the feature of the subway station. Based on a multi-story subway station in Shanghai, a two-dimensional finite element model of the soil and the structure is established and the seismic limit state of the subway station is investigated using the incremental dynamic analysis (IDA). Finally, the relation curve between the seismic intensity measure PBA (peak acceleration at the base of subway station) and structural performance indictorθmax is established and the thresholds ofθmax for this subway station are obtained in the four limit states.

Key words: subway station; performance-based design; limit state; incremental dynamic analysis; performance indicator

性能设计 在结构抗震设计领域的进展显著, 逐步成为新一代工程结构抗震设计的框架. 结构抗震极限状态的确定作为实现该框架的基础起到了至关重要的作用, 在国内外相关规范中给出了地表结构的取值范围[1, 2].

单次动力时程分析只能给出给定地震动强度和特征的结构动力响应, 不足以充分激发结构各阶段的性能. 增量动力分析方法 扩展 了动力时程分析的方式, 可以考察地震动的随机性以及结构在强震下的动力响应, 较为准确地描述结构从弹性、弹塑性直至倒塌的 全过程性能[3], 较广泛地应用于地表结构的抗震性能分析, 如FEMA350给出了依据增量动力分析结果定义结构极限状态的方法, 将地表结构的极限状态分为两个等级：立即使用和防止倒塌, 其中将增量动力曲线斜率下降至曲线弹性斜率的20％定义为防止倒塌极限点[2], 该结论已被广泛应用到地表结构的抗震性能评估中[3, 4, 5]. 地下结构抗震性能的相关研究十分有限. 由于周围土体的存在, 地下结构的动力特性与地表结构必然存在差异, 简单沿用地面建筑结构的性能指标不尽合理.

本文以上海某四层三跨地铁车站的结构为研究背景, 结合地表结构抗震极限状态的基本定义方法[6], 分析地铁车站极限状态的定义方法和表征指标; 根据地下结构自身特点开展地下结构增量动力分析方法研究, 考察地震动记录选择方式、土与结构动力有限元模型建模方法及边界条件设置等. 在有效获得车站结构地震响应的基础上, 研究地震动强度指标( IM)、结构破坏指标( DM)等的表征方式, 以建立该地铁车站对应各个极限状态的定量描述.

1 算例
1.1 工程背景

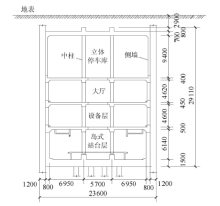
如图1所示, 地铁车站截面为23.6 m宽, 29.11 m高的矩形钢筋混凝土框架. 该车站原设计为六层地铁车站, 后因为停车需要, 将地下一至三层合并为一层, 作为立体停车库. 地下二层为大厅, 地下三层为设备层, 底层为岛式站台层. 地下一层和二层的中柱尺寸为1.1 m ×0.7 m, 而第三层和底层的中柱尺寸为1.4 m ×0.7 m. 中柱沿车站纵向间距为8 m, 埋深2.9 m. 工程地勘报告提供的该车站的土层性质, 如表1所示.

图1 地铁车站的横断面图(单位：mm)

表1 地铁车站土层参数
1.2 有限元模型

依据该地铁车站的工程背景, 本文采用大型有限元软件ABAQUS建立了该地铁车站结构和其周围土体的二维有限元模型. 该软件能够准确 计算结构从弹性到弹塑性的动力响应特性, 并且能够考虑材料非线性和几何非线性[7]. 有限元模型尺寸为长1 000 m, 宽60 m, 如图2所示. 对于结构的单元选取, 采用梁单元B21模拟, 该单元可以较好 地模拟结构的受力和变形[8]. 依据地铁车站的工程项目资料, 混凝土和钢筋的材料属性如表2所示.

图2 有限元模型

表2 地铁车站材料参数

采用Lubliner等[9]和Lee等[10]提出的混凝土塑性损伤模型考虑混凝土的弹塑性, 该塑性损伤模型采用两个损伤变量(即：受 拉损伤和受压损伤). 钢筋通过rebar命令在二维有限元模型中嵌入, 钢筋的本构模型采用具有双线性骨架曲线的Menegotto-Pinto模型[11]. 该模型为各向同性应变硬化1 土体部分采用四节点平面应变单元CPE4R和四边形平面应变无限元CINPE4来模拟土单元. 采用摩尔库伦模型来模拟土体的塑性. 土体的 基本参数如表1所示. 土体和结构间的接触采用摩擦接触, 摩擦系数 μ为0.4, 摩擦角为22° .土和结构之间无粘结.

有限元模型的边界条件为：底部边界的水平和竖向位移均为固定约束, 模型顶部为自由端, 模型两侧边界采用无限元, 地震动在模 型底部输入.

1.3 地震波的选取

地震波的选取主要依据结构所处的场地类别进行. 根据我国抗震规范对场地类别的划分[1], 本文研究地铁车站的场地类别 属于IV类场地. 因此, 本文所选取地震波的场地特征与上海场地相近. 对地震波选取数量, Shome等[13]提出10 ~20条地震波通常可以较为充分地评估结构的动力需求. 根据上述分析, 本文从太平洋地震工程研究中心[14]选取了12条地震波进行增量动力分析, 地震动记录相关信息列于表3.

表3 所选取的12条地震动记录
1.4 IM和 DM的选取

增量动力分析方法的基本原理是对结构施加一个或多个地震动记录, 对每一条地震动记录乘以一系列比例系数, 从而调幅成为具有多重 强度水平的一系列地震动记录; 计算结构在这组调幅地震动作用下的非线性动力时程反应[3]. 选择合适的 IM和 DM得到一系列 IM-- DM曲线, 即为增量动力 曲线. 最后依据增量动力分析计算结果对结构进行抗震性能评估.

其中, 进行增量动力分析较为重要的环节之一即选择合适的 IM和 DM. IM是用来表征地震动强度的参数, IM选取的基本原则是能够 直接反映地震动潜在的破坏效应并且能够使得不同地震动强度下的 DM差异最小. 考虑到结构底部峰值加速度能够直接反映结构所承受的地震动载荷, 因此本文增量动力 分析中采用车站结构底部的峰值加速度( PBA)作为 IM. 对于其他 IM选择下的增量动力 分析结果, 请参见文献[15].

DM是用来表征在地震作用下结构破坏程度的参数, 包括结构构件、非结构构件和内部设施. 它的选取应根据结构的用途和其自身的 特性确定. 考虑到地铁车站结构的最大层间位移角 θmax能够较好反映节点转动以及结构的变形性能, 因此, 在后续增量动力分析 中将 θmax作为 DM指标.

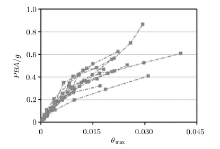
为了得到结构从弹性到弹塑性直至倒塌的全过程动力响应, 将表3中的每条原始地震动记录按一定的比例系数进行调幅, 使得峰 值速度 PGV分别等于3, 5, 10, 20, 30, 40, 50, 60, 70, 80 cm/s, 并计算相应的地震动强度指标 IM. 在每个强度水平下分别进行时程分析. 其中, 地震动沿数值模型(图2)底部水平向输入. 依据其他 IM指标进行地震动调幅的算例将在今后的研究中考虑, 本文仅依据 PGV对地震动调幅.

2 增量动力分析计算结果

依据上述增量动力分析方法实施流程, 对该四层三跨地铁车站结构进行增量动力 分析. 增量动力 曲线如图3所示. 由图可知, 尽管相同 结构和土层条件在不同地震动输入下得到的增量动力 曲线存在差异, 但每条增量动力 曲线的变化趋势相近.

图3 增量动力曲线

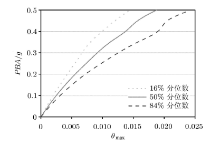
与地表结构不同, 地铁车站的增量动力 曲线没有明显的水平阶段, 如图3所示, 这一现象可以解释为车站周围土体限制了结构的侧向变形. θmax随着地震动强度的提高而不断增大且曲线的斜率不断减小, 但斜率下降幅度十分有限.

由于增量动力 曲线簇中包括大量数据, 且不同地震波的增量动力 曲线存在差异, 因此, 一般地, 将增量动力 曲线簇整理成16根据文献[16], 首先假定 DM对 IM的条件概率分布满足对数正态分布, 其中 μ为 ln(DM)的平均值, σ为 ln(DM)的标准差, 则16％, 50％, 84％分位数曲线所对应的DM值分别为$e^{(\mu-\sigma)}$, $e^\mu$, $e^{(\mu+\sigma)}$. 基于以上假定, 可以绘制出不同 IM的增量动力分析计算结果的16％, 50％和84％分位数曲线, 由图4所示, 由图可知, 代表结构平均动力响应的50结构增量动力分析曲线出现的水平阶段呈现明显差异[3]. 此外, 从图4可以得到任意 PBA所对应 θmax的各分位数值. 例如, 当 PBA=0.3g时, 所对应的16％, 50％和84％分位 θmax分别为0.0067, 0.0092和0.0125, 说明当PBA=0.3g时, 有84％的地震动记录使该结构的 θmax大于0.0067; 同理, 分别有50% 和16% 的地震动记录使该结构的 θmax大于0.009 2 和0.012 5.

图4 增量动力分位数曲线

3 极限状态的定义

极限状态表示结构在特定的某一级地震动强度水平下预期损伤的最大程度. 极限状态的定义是抗震性能评估的必要环节, 将地震发生时所容许的受损程度根据结构抗震极限状态进行不同的规定, 即为对应于该结构抗震极限状态的性能要求. 本节首先定义地铁车站的极限状态, 然后依据增量动力计算结果给出相应各极限状态的 DM界限值.

3.1 极限状态定性描述

对地表结构, FEMA273将结构的极限状态划分为4个层面：正常使用极限状态(结构能够保证正常使用), 轻微破坏(在简单的修复后可以确保结构的使用性), 生命安全(结构出现严重破坏并且需要大量维修才能恢复正常使用)和防止倒塌(结构的功能很难通过维修恢复, 但没有倒塌)[6]. 由以上定义, 本研究从地铁车站自身的受力特性和结构特点对该类结构的抗震极限状态进行定义, 同样考虑以上4个极限状态. 通常, 地铁车站结构的抗震极限状态可以从安全性、使用性、耐久性3个方面进行定义. 同地表结构, 地铁车站结构的安全性可以从结构构件的变形和破坏程度(如中柱柱端位移角)来衡量; 考虑到地铁车站结构的防水性会 直接影响地下结构的使用性和耐久性, 因此, 采用混凝土裂缝宽度来表征结构的止水性能、并进一步作为衡量结构使用性和耐久性的指标. 根据上述分析, 表4给出了4种抗震极限状态的定性描述, 其中每个极限状态都代表地铁车站结构的一个抗震性能水平.

表4 地铁车站抗震极限状态划分
3.2 采用增量动力 曲线判定抗震极限状态

目前, 根据增量动力 曲线判定地表结构的抗震极限状态的相关研究相对成熟, 主要依据增量动力分析曲线斜率的变化趋势对结构的 极限状态进行判定. 例如, FEMA350将地表结构的极限状态依据增量动力 曲线的变化趋势定义为：当曲线斜率达到0.2倍的弹性斜率时, 认为结构处于防止倒塌的极限状态. 然而, 从地铁车站结构的增量动力 曲线结果, 由图3可知, 由于受到周围土体的约束, 地铁车站结构的变形受到制约, 得到的增量动力 曲线斜率下降程度降低, 达不到0.2倍弹性斜率. 因此, 对地铁车站结构抗震极限状态的定义不能直接沿用地表结构的结论.

依据上述分析, 本文提出 地铁车站结构采用增量动力分析 的抗震极限状态判定方法. 首先, 为 定量表述地铁车站结构的安全性, 考虑从结构的变形指标来衡量. 而对地铁车站结构, 中柱作为一个至关重要的构件, 其破坏状态对结构整体起到了决定性作用, 因此, 本文考虑将地铁车站中柱的最 大柱端位移角作为衡量结构变形的指标, 用 θc表示. 其次, 考虑通过地铁车站结构的止水性能来反映结构的使用性和耐久性, 用结构的最大裂缝宽度进行定量描述. 依据《地铁设计规范(GB 50157— 2013)》[17]中第11.6.1条对地铁车站结构最大裂缝宽度的规定, 当最大裂缝宽度超过0.2 mm时, 结构的止水性能失效. 因此, 如何通过有限元模拟得到结构的最大裂缝宽度成为解决该定量描述的核心问题. 本研究发现, 在 ABAQUS有限元模拟中所采用的混凝土塑性损伤模型是建立在受拉损伤( DT)和受拉应变的基础上的, 而 DT是可以从ABAQUS模拟结果中 进行提取的, 从而可以推出相应的受拉应变取值. 同时, 混凝土的裂缝宽度可以通过混凝土单轴受拉试验中拉应变与裂缝宽度的关系得到[18]. 因此, 地铁车站结构抗震极限状态可以依据有限元模拟结果通过中柱的最大柱端位移角 θc和结构最大裂缝宽度进行定量描述. 值得注意的是, 结构的最大裂缝宽度是基于有限元模拟结果中结构受拉损伤最大值 DTmax计算得到的.

根据上述的判定方法, 本文所研究的四层三跨地铁车站的极限状态定量过程如下：

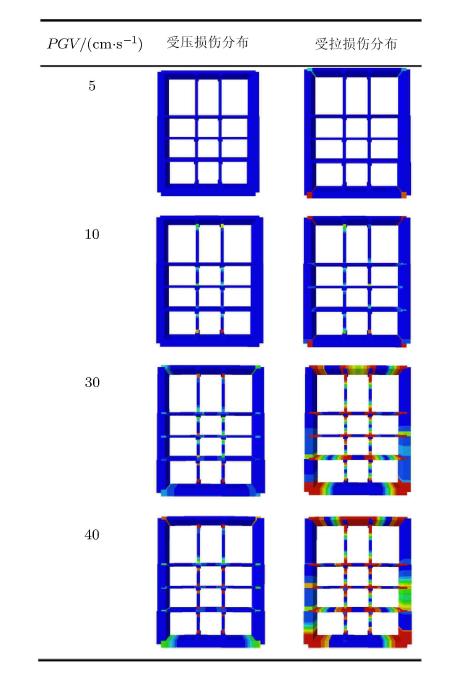
依据增量动力分析结果, 表5给出了地铁车站结构的受压和受拉损伤分布图, 该图来源于与增量动力分析得到的平均动力响应较为 接近的计算工况, 从而考虑了地震动的随机性对结构动力响应的影响. 由图可知, 结构受压损伤分布主要集中在结构中柱和楼板的塑性铰区域, 而结构受拉损伤随着地震动强度的提高发展较为迅速, 从结构楼板向中柱以及侧墙不断发展. 根据受拉损伤分布图可以计算出结构的最大裂缝宽度, 见表6, 其中, DTmax指结构的受拉损伤最大值. 结合《地铁设计规范(GB 50157— 2013)》[17]对地下结构止水失效的裂缝宽度限值0.2 mm, 以及《建筑抗震设计规范(GB 50011— 2010)》[1]中第M.1.3条对框架结构竖向构件(本文即为中柱)柱端位移角 θc的限值规定, 可以发现当调幅地震动强度 PGV分别为5 cm/s, 10 cm/s, 30 cm/s和 40 cm/s时, 该地铁车站分别达到4个极限状态的构件层面限值, 如表7. 因此, 定义4个 PGV地震动强度对应的 DM值为该四层三跨地铁车站的极限状态界限值, 如表8所示.

表5 地铁车站的损伤分布发展
表6 极限状态定量描述指标
表7 中柱柱端位移角 θc的极限状态值[1]
表8 地铁车站的 θmax极限状态限值
4 结 论

本文以上海某四层三跨地铁车站为研究背景, 采用ABAQUS软件建立了土和结构的二维有限元模型, 通过地铁车站的增量动力分析对结构的抗震性能进行判定, 得到以下结论.

(1)由于受到周围土体的约束, 地铁车站结构的变形受到制约, 增量动力 曲线的变化趋势与地表结构不同. 因此, 对地铁车站抗震极限状态的判定不能直接沿用地表结构的方法.

(2)从结构的变形性能和止水性能两个方面定义了地铁车站的4个抗震极限状态. 依据增量动力 分析结果, 提出了地铁车站的抗震极限状态判定方法, 分别通过中柱柱端位移角和裂缝宽度对上述两个性能指标进行定量描述.

(3)本文提出的 θmax极限状态限值为该四层三跨地铁车站的抗震性能评估和设计提供有效依据.

(4)由于本文的分析中仅考虑了单一地铁车站, 因此在后续研究中还将考虑不同形式的地铁车站以得到普适性结论.

The authors have declared that no competing interests exist.

参考文献
[1] GB 50011—2010. 建筑抗震设计规范. 北京: 中国建筑工业出版, 2010 [本文引用:3]
[2] FEMA-350. Recommended seismic evaluation and upgrade criteria for existing welded steel moment-frame buildings. SAC Joint Venture for the Federal Emergency Management Agency, 2000 [本文引用:2]
[3] Vamvatsikos D, Cornell CA. Incremental dynamic analysis. Earthquake Engineering and Structural Dynamics, 2002, 31(3): 491-514 [本文引用:4]
[4] Behrouz A, Mahmood Y, Mirtaheri M, et al. Incremental dynamic analysis of high-rise towers. The Structural Design of Tall and Special Buildings, 2010, 19(8): 922-934 [本文引用:1]
[5] 周颖, 吕西林, 卜一. 增量动力分析法在高层混合结构性能评估中的应用. 同济大学学报(自然科学版), 2010, 38(2): 183-187, 193 [本文引用:1]
[6] FEMA-273. NEHRP Guidelines for the Seismic Rehabilitation of Buildings. The Federal Emergency Management Agency, 1997 [本文引用:2]
[7] ABAQUS, Users Manual V. 6. 10-1. Dassault Systemes Simulia Corp, Providence, RI, 2010 [本文引用:1]
[8] Chen ZY, Chen W, Bian GQ. Seismic performance upgrading for underground structures by introducing shear panel dampers. Advances in Structural Engineering, 2014, 17(9): 1343-1357 [本文引用:1]
[9] Lubliner J, Oliver J, Oller S, et al. A plastic-damage model for concrete. International Journal of Solids and Structures, 1989, 25(3): 299-326 [本文引用:1]
[10] Lee J, Fenves GL. Plastic-damage model for cyclic loading of concrete structures. Journal of Engineering Mechanics, ASCE, 1998, 124(8): 892-900 [本文引用:1]
[11] Menegotto M, Pinto PE. Method of analysis for cyclically loaded RC plane frames including changes in geometry and non-elastic behavior of elements under combined normal force and bending. Symposium on the Resistance and Ultimate Deformability of Structures Acted on by Well Defined Repeated Loads, Zurich, Switzerland , 1973 [本文引用:1]
[12] Elnashai AS, Sarno LD. Fundamentals of Earthquake Engineering. West Sussex (United Kingdom): John Wiley & Sons Ltd, 2010 [本文引用:1]
[13] Shome N, Cornell CA. Probabilistic seismic demand analysis of Nonlinear Structures. Report No. RMS-35, RMS Program, Stanford University, Stanford, 1999 [本文引用:1]
[14] Pacific Earthquake Engineering Research Center (PEER). PEER Strong Motion Database. University of California, 2000 [本文引用:1]
[15] Liu T, Chen ZY, Yuan Y, et al. Fragility analysis of a subway station structure by incremental dynamic analysis. Advances in Structural Engineering, 2016, 20(7): 1111-1124 [本文引用:1]
[16] Jalayer F, Cornell CA. A technical framework for probability-based and capacity factor design (DCFD) seismic formats. Report No. 2003/08, Pacific Earthquake Engineering Research Center, College of Engineering, University of California Berkeley, 2004 [本文引用:1]
[17] GB50157-2013. 地铁设计规范. 北京: 中国建筑工业出版, 2013 [本文引用:2]
[18] 过镇海, 张秀琴. 混凝土受拉应力--变形全曲线的试验研究. 建筑结构学报, 1988(4): 45-53 [本文引用:1]