两端固定的等截面梁在均布载荷作用下的挠曲线
两端固定的等截面梁在均布载荷作用下的挠曲线
题目
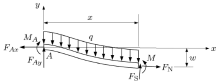
在图1所示的两端固定的等截面梁上作用有均布横向载荷, 设载荷集度为\(q\)、梁的长度为\(l\)、截面惯性矩为\(I\)、横截面积为\(S\)、弹性模量为\(E\), 试在考虑固定端轴向约束力影响的情形下确定该梁的挠曲线函数.
 | 图1 两端固定的等截面梁 |
解题思路
首先画出该梁的受力图(图2). 由静力学平衡方程和对称性原理, 可求出两端的剪力为
\[F_{Ay} = F_{By} = \dfrac{1}{2}ql \ \ (1)\]
 | 图2 梁的受力图 |
为了进一步写出梁在任意横截面上的弯矩表达式, 取坐标为\(x\)的横截面的左端梁为研究对象, 画出该段梁在弯曲变形位置时的受力图(图3), 图中的\({ F }_{\rm N} \), \( { F }_{\rm S}\)和\(M\)分别表示坐标为\(x\)处的横截面上的轴力、剪力和弯矩, \(w\)表示该截面的挠度. 由该段梁的力矩平衡方程可以推得弯矩\(M\)的表达式为\(M= - \dfrac{1}{2}qx^2 + M_A + F_{Ay} x + F_{Ax} w\) , 将该式代入到挠曲线微分方程\(EI {w}" = M\)后, 得到
\[EI{w}" = - \dfrac{1}{2}qx^2 + M_A + F_{Ay} x + \underline{F_{Ax} w} \ \ (2)\]
 | 图3 坐标为 \(x\) 的横截面的左端梁在弯曲变形位置时的受力图 |
式中的画线项\(F_{Ax} w\)代表固定端的轴向约束力\(F_{Ax}\)对于梁的弯曲变形所产生的影响. 固定端的轴向约束力可表达为\(F_{Ax} = F_{Bx} =k \cdot {\Delta } l\), 式中梁的等效拉压刚度\(k = {ES}/l\)和梁的伸长量
这样固定端的轴向约束力可表达为\(F_{Ax} = F_{Bx} = \dfrac{ES}{2l}\int_{ 0}^{ l} {w}'^2 d x\).
\[{\Delta } l = \int_{0}^{ l} \sqrt {1 + {w}'^2} d x - l \approx \int_{ 0}^{ l} \Big(1 +\frac{1}{2}{w}'^2 \Big) d x - l = \frac{1}{2}\int_{ 0}^{l} {w}'^2 d x\]
将该式、固定端\(A\)处的弯矩表达式\(M_A = EI {w}"(0) \)以及式(1)一同代入到式(2)后, 得到
\[EI{w}" = \dfrac{1}{2}qx(l - x) + EI {w}"(0) + \dfrac{ES}{2l}w\int_{ 0}^{ l} {w}'^2 d x \ \ (3)\]这就是两端固定的等截面梁承受均布横向载荷时的挠曲线微积分方程, 该方程中计入了固定端的轴向约束力对于梁的弯曲变形的影响. 考虑到梁的两端均为固定端, 因此, 相应的边界条件为
\[w (0) = 0, \ {w}'(0) = 0, \ w(l) = 0, \ {w}'(l) = 0 \ \ (4)\]
从数学上来讲, 方程(3)且满足边界条件(4)的解就是该梁的挠曲线函数.考虑到方程(3)属于非线性的微积分方程, 要获得其精确 的解析解是非常困难的.为此, 这里应用瑞利-里兹法求近似的解析解. 选取以下两个连续、二阶可导且满足边界条件(4)的函数
\[w_1 (x) = x^4 - 2 lx^3 + l^2x^2 \ \ (5)\]
和
\[w_2 (x) = x^6 - 3 lx^5 + 2 l^2x^4 + l^3x^3 - l^4x^2 \ \ (6)\]
作为瑞利-里兹函数, 这样可以将梁的挠曲线函数近似地表达为
\[w(x) = c_1 w_1 (x) + c_2 w_2 (x) \ \ (7)\]
式中\(c_1 \)和\(c_2\)为两个待定的未知量, 可按如下的方法确定：将式(7)代入方程(3)后, 在方程的两边同乘以\(w_i (x) \ (i = 1, 2)\), 然后再沿梁长取定积分, 化简后, 得到关于\(c_1 \)和\(c_2 \)的两个代数方程
\[968 ESl^8c_1^{3} - 3 608ESl^{10}c_1^{2} c_2 + 4 488ESl^{12}c_1 c_2^{2} + 5 488 560EIc_1 - 1, 863ESl^{14}c_2^{3} -5793480EIl^2c_2 + 228 690q = 0 \ \ (8)\]
\[15 444 ESl^8c_1^{ 3} - 57 574ESl^{10}c_1^{2} c_2 + 71 629ESl^{12}c_1 c_2^{2} + 87 207 120EIc_1 -29 739ESl^{14}c_2^{3} -92 252 160EIl^2c_2 +3 633 630q = 0 \ \ (9)\]
将梁的已知参数和载荷集度代入以上两个代数方程后, 联立求解, 即可得到该组方程的实数解. 设该梁的已知参数如下：长度\(l= 1\) m, 横截面积\(S = 6\times 10^{ -5}\) m\(^{2}\)(宽度为0.02 m, 厚度为0.003 m), 截面惯性矩\(I = 4.5\times 10^{ - 11}\) m\(^4\), 弹性模量\(E = 2.01\times 10^{11}\) Pa. 将梁的这些已知参数和载荷集度\(q=50\) N/m代入方程(8)和(9)后, 联立求解, 得到该组方程的实数解为\(c_1= - 0.271 5\) m\(^{-3}\), \(c_2 = - 0.154 3\) m\(^{-5}\). 最后, 将该组解以及式(5)和式(6)一同代入到式(7)后, 得到
\[w = - x^2(x - 1)^2(0.154 3\; x^2 - 0.154 3\; x + 0.117 2 ) \ \ (10)\]
这就是考虑固定端轴向约束力影响的情形下所得到的该梁的挠曲线函数.
讨论：在一些材料力学教科书中所给出的未考虑固定端轴向约束力影响的该梁的挠曲线函数为
\[w = \dfrac{1}{EI}\Big ( - \dfrac{q}{24}x^4 + \dfrac{ql}{12}x^3 -\dfrac{ql^2}{24}x^2 \Big)\]
将梁的上述已知参数和载荷集度\(q =50\) N/m代入到此式后, 就是
\[w = - 0.230 3\; (x^4 - 2x^3 + x^2) \ \ (11)\]
图4中分别标出了根据式(10)和式(11)所画出的挠曲线.
由图4可以看出：考虑固定端轴向约束力影响的情形下所得到的梁的挠曲线要比未考虑这种影响所得到的梁的挠曲线更加平坦.
因此, 为了更加精准地确定该梁的挠曲线形状, 有必要在分析和计算中考虑固定端轴向约束力的影响.
 | 图4 梁的挠曲线 |
The authors have declared that no competing interests exist.