作者简介:唐有绮, 副教授,主要研究方向为非线性动力学与振动控制. E-mail: tangyouqi2000@163.com
考察了刚性直杆由静止开始倾倒到接触地面前这一短暂时间内的力学行为.建立了刚性直杆定轴转动和平面运动的动力学方程.应用Mathematica软件揭示了系统在倾倒过程中的角位移、角速度、角加速度、质心加速度以及摩擦力等随时间变化的规律.
理论力学是高等理工科院校, 特别是其中的机械工程、轨道交通、城市建设与安全工程、材料工程等学院的一门理论性很强的主干技术基础课, 是一门与工程实际紧密联系的课程, 也是后续力学课程和其他相关专业课程的基础, 在整个教学过程中担负着承前启后的任务, 对培养学生的工程素质起着非常重要的作用.目前, 各大高校理论力学课程还是以理论教学为主, 对于力学模型的分析还是注重瞬时分析, 与生产实践的结合较少.
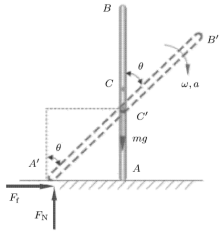
在许多理论力学教材[1, 2, 3, 4, 5]中都有不考虑空气阻力时刚性直杆的倾倒问题, 如图1所示.然而, 目前的教材中都是分 析刚性直杆在理想平面上某一瞬时的力学特性, 尚没有见到关于该模型的过程分析.本文利用理论力学的基本概念, 对刚性直杆在粗糙的平面上由静止开始倾倒到接触地面前这一短暂时间内的运动状态进行过程分析, 动态演示其力学行为.
假设直杆\(AB\)在运动的过程中变形量很小, 故可抽象为刚性杆. 已知刚性直杆与平面间的静滑动
摩擦因数为\(f_{\rm s}\), 动滑动摩擦因数为\(f_{\rm d}\), 长度为\(l\), 质量为\(m\).仅在重力作用下, 刚性直杆无初速下滑. 在\(t\)时刻, 刚性直杆与竖直方向的夹角为\(\theta (t)\), 角速度为\(\omega(t)=d\theta / dt\), 角加速 度为\(\alpha (t)=d^{2} \theta / dt^{2}\).
在当前的理论力学教材中, 均考虑理想情况, 即忽略摩擦力对刚性直杆的影响, 其示意图如图2所示.但是在实际情况中, 摩擦是不可避免的. 本文首先考虑有较大摩擦力的倾倒问题, 刚性直杆在释放的短时间内绕其与平面的接触点做定轴转动.
由质心运动定理知
\[ma_{{ C}x} = F_{\rm f} \ \ (1)\]
\[ma_{{ C}y} = mg - F_{\rm N} \ \ (2)\]
式中, \(a_{{ C}x}\)和\(a_{{ C}y}\)分别为质心加速度\(a_{ C}\)在水平和垂直方向的分量.
由对质心的动量距定理得到
\[J\alpha = \dfrac{ml^2}{12}\ddot {\theta } = \dfrac{F_{\rm N} l\sin \theta}{2} - \dfrac{F_{\rm f}l \cos\theta}{2} \ \ (3)\]
质心的加速度为
\[{\pmb a}_{ C} = {\pmb a}_{{ CA}}^{\rm n} + {\pmb a}_{{ CA}}^{\tau } \ \ (4)\]
质心的加速度\({\pmb a}_{ C} \)的 水平分量(向右为正)和竖直分量(向下为正)为
\[ a_{{ C}x} = - \dfrac{\omega ^2 l\sin \theta }{2}+\dfrac{ \alpha l \cos \theta}{2} = \\ \qquad -\dfrac{\dot {\theta }^2l \sin \theta }{2}+\dfrac{ \ddot {\theta } l \cos \theta }{2} \ \ (5)\]
\[ a_{{C}y } =\dfrac{ \omega ^2 l\cos \theta}{2} +\dfrac{ \alpha l \sin \theta}{2} = \\ \qquad \dfrac{\dot {\theta }^2 l \cos \theta}{2} + \dfrac{ \ddot {\theta } l \sin \theta}{2} \ \ (6)\]
将式(1), (2), (5), (6)代入式(3), 得到
\[\ddot {\theta } - \dfrac{3g}{2l}\sin \theta = 0 \ \ (7)\]
从式(7)可以看出, 在不考虑空气阻力的情况下, 刚性直杆运动的角度、角速度和角加速度均与其质量和横截面尺寸及形状无关, 仅与重力加速度和其长度有关.
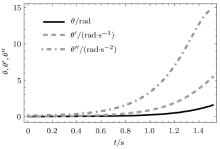
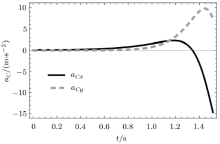
本文考虑的系统相关参数如下:长度\(l=1\) m、重力加速度\(g=9.8\) m/s\(^{2}\)、质量\(m=1\) kg.下面运用Mathematica软件对 系统(7)进行数值求解, 分析系统从开始倾倒到接触地面前, 即在\(0\sim1.513 6\) s这一短暂时间内的力学行为. 给定初始角位移\(\theta (0)=0.01\) rad、初始角速度\(\omega (0)=0\) rad/s.图3给出了刚性直杆的角位移、角速度、角加速度随时间的变化规律.图4给出了刚性直杆质心的水平和竖直加速度随时间的变化规律. 从图中可以看出刚性直杆随时间加速转动.在水平方向上, 刚性直杆的质心随时间加速运动; 而在竖直方向上, 刚性直杆的质心随时间先加速运动再减速运动.
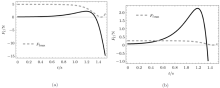
以上分析的结果是基于摩擦较大, 刚性直杆做定轴转动的前提条件.比如木材与木材在无润滑的情况下的静摩擦因数 \(f_{\rm s}\)为0.4\(\sim \)0.6[3], 取\(f_{\rm s} =0.5\).此时解得的 摩擦力\(F_{\rm f}\)和最大静滑动摩擦力\(F_{\rm f\max}\)随时间的变化规律如图5(a)所示.从图中可以看出系统从开始倾倒到接触地面前\(F_{\rm f}\)始终小于\(F_{\rm f\max}\), 刚性直杆做定轴转动的假设成立.
下面我们考虑有小摩擦力时的倾倒问题. 如果我们选用钢与冰, 它们的静摩擦因数为\(f_{\rm s}=0.027\), 动摩擦因数为\(f_{\rm s} =0.014\), 此时\(F_{\rm f}\)和\(F_{\rm f\max}\)随时间的变化规律如图5(b)所示.从图中可以看出系统在\(0 \sim 0.509 76\) s之间\(F_{\rm f} < F_{\rm f\max}\), 刚性直杆做定轴转动的假设成立; 而在\(0.509 76 \sim 1.513 6\) s之间\(F_{\rm f} > F_{\rm f\max}\), 刚性直杆做定轴转动的假设不成立, 实际上这段时间内刚性直杆做平面运动.下面我们以接触点刚发生滑动的瞬间为初始时刻来分析刚性直杆的平面运动.
根据质心运动定理和对质心的动量距定理, 同样可以得到式(1) \(\sim\)式(3). 将质心的加速度\( {\pmb a}_{ C}\)的矢量合成式分别在水平和竖直轴上投影, 得到
\[a_{{C}x} = - a_{\rm A} - \dfrac{\dot {\theta }^2 l \sin \theta }{2}+ \dfrac{\ddot {\theta }l\cos \theta}{2} \ \ (8)\]
\[ a_{{C}y} = \dfrac{\dot {\theta }^2 l \cos \theta}{2} +\dfrac{ \ddot {\theta } l \sin \theta}{2}\ \ (9)\]
此时的摩擦力为动滑动摩擦力
\[F_{\rm d} = f_{\rm d} F_{\rm N} \ \ (10)\]
联立式(1) \(\sim\)式(3), 式(8) \(\sim\)式(10), 得到
\[l\ddot {\theta } = 3\left( {f_{\rm d} \cos \theta - \sin \theta } \right)\left( {l\ddot {\theta }\sin \theta+ l\dot {\theta }^2\cos \theta - 2g} \right) \ \ (11)\]
从式(11)可以看出, 在不考虑空气阻力的情况下, 刚性直杆运动的角度、角速度和角加速度不仅与重力加速度和长度有关, 还与动摩擦因数有关.
从图5(b)中可以得到, 在接触点刚发生滑动的瞬时, 系统的角位移和角速度是本节中系统做平面运动时的初始角位移 \(\theta (0)=0.036 007 4\) rad和初始角速度 \(\omega (0)=0.132 616\) rad/s.
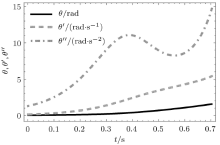
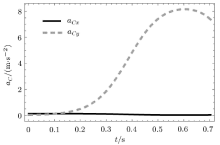
在平面运动的过程中, 系统共历时0.70359s.图6给出了刚性直杆的角位移、角速度、角加速度随时间的变化规律.图7给出了刚性直杆质心的水平和竖直加速度随时间的变化规律.从图中可以看出刚性直杆随时间作加速转动.
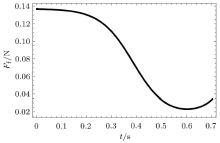
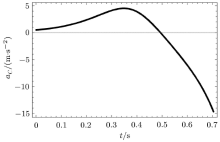
此时刚性直杆的摩擦力\(F_{\rm f}\)和其与地面接触点的加速度\(a_{A}\)随时间的变化规律如图8和图9所示.从图中可以看出, 刚性直杆的摩擦力先减小后增大, 但是方向始终水平向右.其与地面的接触点的加速度先增大后减小, 方向开始水平向左而后水平向右.
特别地, 刚性直杆在完全光滑的平面上时, 可令式(10)中的\(f_{\rm d} =0\), 即可推出与图6 \(\sim\)图8类似的结论.
本文应用理论力学的基本概念建立了刚性直杆的动力学模型, 应用Mathematica软件分析了在倾倒过程中系统参数随时间的变化规律.本文对刚性直杆的过程分析结果将有助于学生牢固掌握理论知识并能灵活运用, 真正把所学应用于工程实际.另外, 在分析过程中引入Mathematica软件, 也有助于学生通过图片和动画的形式更加直观地观察各系统参数随时间的变化规律, 进一步激发学生的学习兴趣.
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|