从中学 就开始了解和学习角速度这个物理量. 认知也从中学的标量,到大学物理中的矢量.本文通过分析刚体一般运动时点的速度和加速度,证明了角速度是二阶张量,同时给出了角速度矢量表达需要满足的条件,明确指出角速度的准确表达必须用张量,角速度的简便表达可以用矢量. 最后讨论了几个与角速度相关的问题.
角速度这个物理量在中学物理中就有, 主要是描述一个质点的匀速圆周运动. 质点的瞬时速度和法线加速度计算公式为\(v =\omega r, \quad a = v^2 / R = \omega ^2R\), 其中\(v\)是点的速度, \(\omega\)是角速度, \(R\)是圆周运动的半径, \(a\)是点的加速度. 这些量都被当作标量对待.
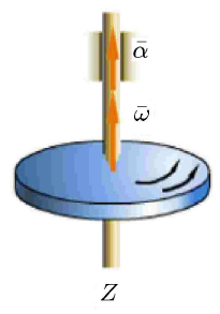
以刚体作定轴转动(转轴为\(z\), 沿\(z\)轴的单位矢量为\({\pmb k}\), 如图1)为例, 转动角度\(\varphi \), 角速度\({\pmb \omega}\), 角加速度\({\pmb \alpha }\)之间的关系
\[{\pmb \omega} = \omega {\pmb k} = \dot {\varphi }{\pmb k}, \quad {\pmb \alpha} = \dot {\pmb \omega } = \dot {\omega }{\pmb k}\]
刚体上一点\(M\)的速度 \({\pmb v}\)和加速度 \({\pmb a}\)与刚体的角速度 \({\pmb \omega }\)和角加速度 \({\pmb \alpha }\) 之间的关系式( 图2 ) 为
\[ {\pmb v }= {\pmb \omega} \times {\pmb r} \\ {\pmb a} = \dot{\pmb v} = \dot{\pmb \omega }\times {\pmb r }+ {\pmb \omega} \times {\pmb v} = {\pmb \alpha} \times {\pmb r} + {\pmb \omega} \times {\pmb v} \]
通过大学物理学习, 学生知道这些物理量都是矢量, 中学物理只是学习其中一种特殊情况的标量解答.至今角速度作为矢量被普遍认可.
在理论力学教学中, 有两种方式引入角速度. 一种是延续和推广大学物理中的认知, 另一种作为张量引入.《张量分析》[1]对张量作了严格的定义.由若干有序数组成的集合, 其表征不随坐标系的改变而改变, 称这个集合为张量. 显然, 标量是零阶张量, 矢量是一阶张量.
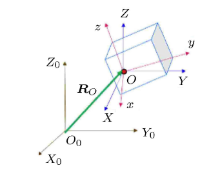
设在\(t\)时刻长方体(刚体)位置如图3所示, 刚体一般运动可以分解成随基点\(O\)的平行移动加上绕基点\(O\)的定点运动.建立如下3个笛卡尔直角坐标系:固定系\(O_{0}X_{0}Y_{0}Z_{0}\) (\({\pmb i}_{0}, {\pmb j}_{0}, {\pmb k}_{0})\); 固连系(固连在刚体上)\(Oxyz ({\pmb i}', {\pmb j}', {\pmb k}')\); 平动系(相对于固定系) \(OXYZ({\pmb i}, {\pmb j}, {\pmb k})\)\(^{[2\hbox{-}3]}\).
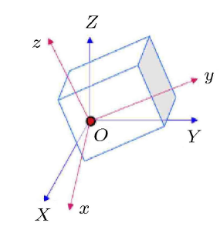
\({\pmb A}={\pmb A}(t)\)是坐标系\(Oxyz\)相对于坐标系\(OXYZ\)方向余弦阵, 如图4.
\[ {\pmb A}=\left[\begin{array}{ccc} a_{11} \ \ a_{12} \ \ a_{13} \\ a_{21} \ \ a_{22} \ \ a_{23} \\ a_{31} \ \ a_{32} \ \ a_{33}\end{array} \right]= \left[\begin{array}{ccc}{\pmb i}\cdot{\pmb i}' \ \ {\pmb i}\cdot{\pmb j}' \ \ {\pmb i}\cdot{\pmb k}' \\ {\pmb j}\cdot{\pmb i}' \ \ {\pmb j}\cdot{\pmb j}' \ \ {\pmb j}\cdot{\pmb k}'\\ {\pmb k}\cdot{\pmb i}' \ \ {\pmb k}\cdot{\pmb j}' \ \ {\pmb k}\cdot{\pmb k}'\end{array}\right]\]
显然\({\pmb A}\)是正交矩阵, 满足关系式\({\pmb A}^{\rm T}{\pmb A} ={\pmb I}\), \({\pmb A}^{\rm T}={\pmb A}^{ - 1}\).
根据刚体在\(t\)时刻(图5)位置, 得到刚体上点\(P\)的运动方程(在\(O_{0}X_{0}Y_{0}Z_{0} ({\pmb i}_{0}\), \({\pmb j}_{0}\), \({\pmb k}_{0}\))下)
\[{\pmb R} ={\pmb R}_O +{\pmb r} \ \ (1)\]
假设\(\underline {\pmb R}\), \(\underline {\pmb R}_{O}\), \(\underline {\pmb r}\)分别是\({\pmb R}, {\pmb R}_{O}\), \({\pmb r}\)在坐标系\(O_{0}X_{0}Y_{0}Z_{0}\)下的坐标列阵, \(\underline{\pmb \rho}\)是\({\pmb r}\)在坐标系\(Oxyz\)下的坐标列阵, \(\underline{\pmb \rho}\)在刚体运动过程中, 保持不变, 是常数列阵. 于是有
\[\underline{\pmb r}= {\pmb A} \underline{\pmb \rho}, \ \ \underline{\pmb \rho}={\pmb A}^{\rm T}\underline {\pmb r}\]
于是式(1)可以改写为
\[\underline{\pmb R}=\underline{\pmb R}_O+\underline{\pmb r}=\underline{\pmb R}_O+{\pmb A}\underline{\pmb \rho}\ \ (2)\]
式(2)对时间求导数(在\(O_{0}X_{0}Y_{0}Z_{0}\)(\({\pmb i}_{0}\), \({\pmb j}_{0}\), \({\pmb k}_{0}\))下), 得到刚体上点\(P\)的速度和加速度表达式
\[\left.\begin{array}{l} \dot{\underline{\pmb R}}= \dot{\underline{\pmb R}}_O + \dot {\underline{\pmb r}} = \dot {\underline{\pmb R}}_O + \dot {\pmb A}\underline{\pmb \rho } +{\pmb A}\dot {\underline{\pmb \rho }} = \dot {\underline{\pmb R} }_O + \dot {\pmb A}{\pmb A}^{\rm T}\underline{{\pmb r}}\\ \ddot{\underline{\pmb R}} = \ddot {\underline{\pmb R}} _O + \ddot {\underline{\pmb r}} =\ddot {\underline{\pmb R}}_O + \ddot{\pmb A}\underline{\pmb \rho } = \ddot {\underline{\pmb R} } _O + \ddot {\pmb A}{\pmb A}^{\rm T}\underline{\pmb r} \end{array}\right\} \ \ (3)\]
将式\({\pmb A}{\pmb A}^{\rm T}={\pmb I}\) 两边对时间求导\[\dfrac{d}{d t}\left( {{\pmb A}{\pmb A}^{\rm T}} \right) = \dot{\pmb A}{\pmb A}^{\rm T} + {\pmb A} \dot{\pmb A}^{\rm T} = \dot{\pmb A}{\pmb A}^{\rm T} + \left( {\dot{\pmb A}{\pmb A}^{\rm T}} \right)^{\rm T} ={\bf 0}\]
可知\(\dot{\pmb A}{\pmb A}^{\rm T}\) (记为矩阵\({\pmb \Omega} \))是坐标系\(O_{0}X_{0}Y_{0}Z_{0}\) \(( {\pmb i}_{0}\), \({\pmb j}_{0}\), \({\pmb k}_{0}\))下的反对称矩阵
\[{\pmb \varOmega} = \dot{\pmb A}{\pmb A}^{\rm T}=\left[\begin{array}{ccc} 0 & -\omega_z & \omega_y \\ \omega_z & 0 & -\omega_x \\ -\omega_y & \omega_x & 0\end{array} \right] \ \ (4)\]
其中
\[\omega_x= a_{21} \dfrac{da_{31}}{dt}+ a_{22} \dfrac{da_{32}}{dt}+ a_{23} \dfrac{da_{33}}{dt} =\\ \qquad -\Big(a_{31} \dfrac{da_{21}}{dt}+ a_{32} \dfrac{da_{22}}{dt}+ a_{33} \dfrac{da_{23}}{dt}\Big) \\ \omega_y=a_{31} \dfrac{da_{11}}{dt}+ a_{32} \dfrac{da_{12}}{dt}+ a_{33}\dfrac{da_{13}}{dt} =\\ \qquad -\Big (a_{11} \dfrac{da_{31}}{dt}+ a_{12} \dfrac{da_{32}}{dt}+ a_{13} \dfrac{da_{33}}{dt} \Big )\\ \omega_z=a_{11} \dfrac{da_{21}}{dt}+ a_{12} \dfrac{da_{22}}{dt}+ a_{13} \dfrac{da_{23}}{dt} =\\ \qquad -\Big (a_{21} \dfrac{da_{11}}{dt}+ a_{22}\dfrac{da_{12}}{dt}+ a_{23} \dfrac{da_{13}}{dt} \Big) \]
我们很容易证明\({\pmb \varOmega} \) 是张量. 刚体一般运动中, 随基点的平行移动部分不影响转动效果, 因此为了单独分析 \({\pmb \varOmega }\)的性质, 假设刚体作定点运动(如图4), 由 式(3)有\(\dot {\underline{\pmb r}} ={\pmb \varOmega} \underline{\pmb r}\), 即
\[{\pmb v} = {\pmb \varOmega} \cdot {\pmb r} \ \ (5)\]
速度\({\pmb v}\)和矢径\({\pmb r}\)都是矢量, 即一阶张量, 根据张量的商法则, 可知 \({\pmb \varOmega }\)是一个二阶张量.因为 \({\pmb \varOmega }\)与刚体的转动相关, 也称为转动角速度张量. 证明完毕.
因为矩阵\({\pmb \varOmega} \)是反对称的, 所以也称 \({\pmb \varOmega } \) 为二阶反对称张量.反对称矩阵\({\pmb \varOmega} \) 只有3个元素独立, 由张量分析[1]可知, 它对应着在同一个坐标系下的(相伴)矢量\({\pmb \omega} \)\(^{[2\hbox{-}3]}\)
\[{\pmb \omega} = {\pmb \omega} _x {\pmb i}_0 + {\pmb \omega }_y {\pmb j}_0 +{\pmb \omega} _z {\pmb k}_0\ \ (6)\]
二阶反对称张量\({\pmb \varOmega} \), 可以用其(相伴)矢量 \({\pmb \omega }\)代替, 它们之间满足如下关系[1]
\[{\pmb \varOmega } \cdot {\pmb r} = {\pmb \omega} \times {\pmb r}, \quad \dot{\pmb \varOmega } \cdot {\pmb r} = \dot {\pmb \omega }\times {\pmb r} \ \ (7)\]
其中\({\pmb r}\)是任意矢量.
由式(1), 式(3) \(\sim\)式(7), 整理得刚体一般运动, 刚体上\(P\)点的速度和加速度为
\[{\pmb v} ={\pmb v}_O + {\pmb \varOmega } \cdot {\pmb r} = {\pmb v}_O + {\pmb \omega}\times {\pmb r} \ \ (8)\]
\[{\pmb a} = {\pmb a}_O + \left( { \dot{\pmb \varOmega } + {\pmb \varOmega }^2}\right) \cdot {\pmb r} = {\pmb a}_O + \dot{\pmb \omega }\times {\pmb r} + {\pmb \omega }\times \left( {{\pmb \omega} \times {\pmb r}} \right) \ \ (9)\]
从\(P\)点的运动公式中得出:二阶反对称张量 \({\pmb \varOmega }\)的矢量表达\({\pmb \omega}\)就是大家熟悉的角速度.
如果刚体一般运动退化成定轴转动 (转轴为\(z\)轴, 绕\(z\)轴旋转角度\(\varphi \)), 如图1所示, 此时矩阵\({\pmb A}\)、矩阵\({\pmb \varOmega } \)以及\({\pmb \omega} \)和\({\pmb \alpha }\)简化为
\[{\pmb A} = \left[ \begin{array}{ccc} {\cos \varphi } & { - \sin \varphi } & 0 \\ {\sin \varphi } & {\cos \varphi } & 0 \\ 0 & 0 & 1 \end{array} \right], \quad {\pmb \varOmega } = \left[\begin{array}{ccc} 0 & { - \omega _z } & 0 \\ {\omega _z } & 0 & 0 \\ 0 & 0 & 0 \end{array} \right]\]
\[{\pmb \omega} = \omega _z {\pmb k }= \dot {\varphi }{\pmb k}, {\pmb \alpha }= \dot {\pmb \omega } = \dot {\omega }_z {\pmb k}\]
刚体上点\(P\)的运动量结果简化为
\[ {\pmb v} = {\pmb \omega} \times {\pmb r}\\ {\pmb a }= \dot {\pmb v} = \dot {\pmb \omega }\times{\pmb r} + {\pmb \omega} \times \dot {\pmb r} = \dot {\pmb \alpha }\times{\pmb r} + {\pmb \omega} \times {\pmb v}\]
得到的公式与在大学物理中学习的公式一致.
在一般情况下, 角速度这个物理量 数学上可以用矢量 \({\pmb \omega } \)描述, 但有些情况下会出现问题. 用张量 \({\pmb \varOmega } \) 描述角速度在数学上最准确, 任何情况下都不会有问题.
在北京大学的朱照宣先生主编的《理论力学》上册 指出[4]:一个矢量必须满足其表达式与坐标系 选择无关的条件.分析\({\pmb v} ={\pmb \omega}\times {\pmb r}\), 其中\({\pmb v}\)和\({\pmb r}\)都是矢量, 与坐标系选择无关. 在研究由右手系到左手系(或者左手系到右手系)这种坐标变换 时, 得出\({\pmb v}'={\pmb r}' \times {\pmb \omega}'\), 表达式发生改变, 无法满足其与坐标系选择无关这个条件. 问题就出在角速度上. 所以说, 要想把角 速度看成矢量, 就必须对坐标变换作说明或者限定, 如果只考虑由右手系到右手系的变换, 角速度可以当成矢量应用. 如果角速度用张量\({\pmb \varOmega }\)表示, 无论是右手系到右手系间的转换, 还是右手系到左手系的转换等, 表达式都不会改变.
在周培源先生编写的《理论力学》 也强调[5]:刚体的有限转动虽不能用向量代表, 但可以用并矢(二阶张量)来描写, 即
\[ {\pmb r}_1 - {\pmb r} = (1 - \cos \theta )( {\pmb r}\times {\pmb n}{\pmb n} - {\pmb r}) + \sin \theta {\pmb n}\times {\pmb r}\]
假如 \(\theta \) 的数值甚小, 则右边的第一项可以不计.这说明有限转动必须用张量描述, 无限小转动可以近似地用向量描述.
因此, 角速度的准确表达必须用张量, 角速度的简便表达可以用矢量. 理论力学中可以把角速度看作矢量[2].
角速度本质是二阶张量, 人们为什么还是喜欢用矢量描述角速度呢?其原因大致有:(1) 历史原因; (2)在教学中符合学生认识水平和数学基础等考虑; (3)在工程应用中更简洁, 一般不会出问题, (4) 对这个概念认识的历史上传统看法与习惯等.
对于刚体的定点运动(图4), 方向余弦矩阵\({\pmb A}\)还可以通过欧拉角(\(\varPsi \), \(\theta \), \(\varphi\))三次转动坐标系得到: 第一次由\(OXYZ\) (\({\pmb i}\), \({\pmb j}\), \({\pmb k}\))绕\(Z\)轴转动角度 \(\psi \)(进动角)到\(Ox_{1}y_{1}z_{1}\) (\({\pmb i}_{1}\), \({\pmb j}_{1}\), \({\pmb k}_{1}\)) (图6(a)); 第二次由\({Ox}_{1}y_{1}z_{1}\)绕\(x_{1}\)轴转动角度\(\theta \) (章动角)到\({Ox}_{2}y_{2}z_{2}\)(\({i}_{2}\), \({j}_{2}\), \({k}_{2}\)) (图6(b)); 第三次由\( Ox_{2}y_{2}z_{2}\)绕\(z_{2}\)轴转动角度\(\varphi\) (自动角)到\({Ox}_{3}y_{3}z_{3}\)(\({\pmb i}_{3}\), \( {\pmb j}_{3}\), \({\pmb k}_{3}\)) (\(Oxyz\) (\({\pmb i}', {\pmb j}', {\pmb k}')\))(图6(c))\(^{[2\hbox{-}3, 6]}\).
三次转动的方向余弦矩阵分别为
\[{\pmb A}_1=\left[ \begin{array}{ccc} \cos\psi \ \ \ -\sin\psi \ \ 0 \\ \sin\psi \ \ \cos \psi \ \ 0 \\ 0 \ \ 0 \ \ 1\end{array} \right]\\ {\pmb A}_2=\left[ \begin{array}{ccc}1\ \ 0 \ \ 0 \\ 0 \ \ \cos\theta \ \ -\sin \theta \\ 0 \ \ \sin \theta \ \ \cos \theta \end{array} \right] \\ {\pmb A}_3=\left[ \begin{array}{ccc} \cos\varphi \ \ -\sin\varphi \ \ 0 \\ \sin\varphi \ \ \cos\varphi \ \ 0\\ 0 \ \ 0 \ \ 1 \end{array}\right] \]
\[{\pmb A} = {\pmb A}_1 {\pmb A}_2 {\pmb A}_3 \ \ (10)\]
把 式(10)代入 式(4), 整理得到用欧拉角描述刚体在坐标系\({Oxyz}\) (或\({Ox}_{3}y_{3}z_{3})\)下的\({\pmb \omega}\)坐标列阵为
\[\left(\begin{array}{l} \omega _1 \\ \omega _2 \\ \omega _3 \end{array}\right)={\pmb A}^{\rm T} \left(\begin{array}{c}\omega_x \\ \omega_y \\ \omega_z\end{array}\right)= \left(\begin{array}{c}\dot\psi \sin\theta \sin \varphi +\dot\theta\cos\varphi \\ \dot\psi \sin\theta \cos \varphi-\dot\theta\sin\varphi \\ \dot\psi\cos \theta+\dot\varphi \end{array}\right)\]
\[\omega ^2 = \omega^2_1+\omega^2_2+\omega^2_3= \dot {\psi }^2 + \dot {\varphi }^2 + \dot {\theta }^2 + 2\dot{\psi }\dot {\varphi }\cos \theta \ \ (11)\]
同时可求出
\[\left(\begin{array}{l} \dot {\psi } \\ \dot {\theta } \\ \dot {\varphi } \end{array}\right) =\left(\begin{array}{c}(\omega_1\sin\varphi +\omega_2\cos\varphi)/\sin\theta \\ \omega_1\cos\varphi-\omega_2\sin\varphi\\ \omega_3-(\omega_1\sin\varphi+\omega_2\cos\varphi) {\rm cot}\theta \end{array}\right)\]
根据角速度合成定理[4], 上述三次坐标系旋转的角速度有
\[ \mathop {\lim }\limits_{\Delta t \to 0} (\Delta {\pmb \beta} / \Delta t) = {\pmb \omega }= \\ \qquad\omega _\varphi {\pmb k}_2 + \omega _\theta {\pmb i}_1 + \omega _\psi {\pmb k} = \dot {\varphi } {\pmb k}_2 +\dot {\theta }{\pmb i}_1 + \dot {\psi }{\pmb k} \ \ (12)\]
由式(11)得
\[ \left( {\omega dt} \right)^2 = \left( {d\psi } \right)^2 + \left( {d\varphi } \right)^2 + \left({d\theta } \right)^2 + \qquad 2d\psi d\varphi \cos \theta \ \ (13)\]
但是式(13)无法写成全微分. 即
\[ \left( {\omega dt} \right)^2 = \left( {d\psi } \right)^2 + \left( {d\varphi } \right)^2 + \left({d\theta } \right)^2 + \qquad 2d\psi d\varphi \cos \theta \ne \underline{(\dot {\beta }dt)^2 =(d\beta )^2} \ \ (14)\]
通过以上分析及式(12)和式(14)有下面结论:
(1) 分析力学中定义``准速度''为广义速度的线性组合, 其在一定条件下才能写成全微分.这也是引入``准坐标''概念的原因[7];
(2) 角速度是广义速度的非线性组合, 一般不存在标量函数 \(\beta (t)\), 即角速度的大小不能表示成\(\omega =d\beta/d t\);
(3) 只有运动退化为定轴转动时, 标量函数 \(\beta (t)\)才存在, 且 \(\dot\beta=\dot\varphi\);
(4) 矢量式的极限存在\(\mathop {\lim }\limits_{\Delta t \to 0} (\Delta {\pmb \beta} / \Delta t) = \dot {\varphi}{\pmb k}_2 + \dot {\theta }{\pmb i}_1 + \dot {\psi }{\pmb k}\);
(5) 刚体一般运动的角速度与定点运动类似, 平面运动的角速度与定轴转动类似.
所谓刚体的瞬时转轴(简称瞬轴)是指在\(t\)时刻, 刚体上如果有两点的瞬时(绝对)速度为零, 那么这两点连线就是刚体的瞬时转轴.
显而易见, 式(4)矩阵\({\pmb \varOmega} \)的det\({\pmb \varOmega} =0\); 矩阵\({\pmb \varOmega}\)特征值为零和一对纯虚根, 因此其零空间是一维的, 即直线. 由此可知:
(1)刚体定点转动时, 方程\({\pmb v} = {\pmb \varOmega } \cdot {\pmb r}\)有无穷多解, 因此定点运动刚体瞬轴存在且唯一, 与矢量 \({\pmb \omega } \) 共线.
(2)刚体一般运动时, 方程\( {\pmb \varOmega } \cdot {\pmb r} =-{\pmb v}_O+{\pmb v}= {\pmb v}_O ( \ne {\pmb 0})\)可能无解, 即可能不存在瞬心和瞬轴. 实例:作螺旋运动的炮弹, 没有任何一点的瞬时速度为零.
(3)刚体作平面(\(Oxy\)面内)运动时, 方程 \( {\pmb \varOmega } \cdot {\pmb r} = -{\pmb v}_O+{\pmb v}={\pmb v}_O (\ne {\bf 0})\), 可以简化为
$$\left [ \begin{array}{ccc} 0 & { - \omega _z } & 0 \\ {\omega _z } & 0 & 0 \\ 0 & 0 & 0\end{array}\right]\left( \begin{array}{c} x \\ y \\ z\end{array} \right) = \left( \begin{array}{c} { - v_{Ox} } \\ { - v_{Oy} } \\ 0 \end{array} \right)$$
解空间是一维, 是垂直于\(xy\)平面的直线. 在\(xy\)平面上体现为一个点, 即瞬心. 即平面运动的刚体瞬轴存在且唯一.
对角速度的认知从点的匀速圆周运动到刚体的定轴转动, 从刚体的定轴转动到平面运动, 从刚体的平面运动到定点运动及一般运动, 历经了几次飞跃.本文对刚体角速度进行分析和思考后有如下体会:角速度准确表达要用张量, 如果不涉及左手系到右手系之间的变换, 可以简便表达成矢量; 角速度不一定能表示成角度对时间的导数; 刚体是否存在瞬时转轴要具体看刚体的运动方式.刚体角速度情况总结见表1.
| 表1 刚体角速度情况总结 |
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|