二自由度动力消振器是振动力学课程中讲述多自由度系统受迫振动时常举的例题[1], 也在工程实践中得到实际应用.如楼高448m的台北101大楼的摆式动力消振器, 其摆锤质量662t, 摆长11.5m, 固有频率约0.15Hz, 接近大楼的基频.在阵风作用下可避免大楼产生基频附近的谐振(图1)[2]. 近期建造完工的上海中心大楼高度632m, 是世界第二高楼.为减小风载引起的晃动也采用了动力消振器, 但增加了电磁涡流阻尼器以加强能量耗散(图2)[3].动力消振器的工作原理基于二自由度线性系统的无阻尼受迫振动.为了解阻尼器的出现对消振器工作原理的影响, 本文对振动力学的这个典型例题作些补充分析.
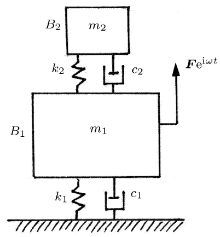
设二自由度系统由建筑物\(B_1 \)和建筑物内安装的消振器\(B_2 \)构成. \(B_1\)的质量为\(m_1 \), 受刚度系数\(k_1 \), 阻尼系数\(c_1 \)的弹性地基支承. \(B_2\)的质量为\(m_2 \), 以刚度系数\(k_2 \)的弹簧和阻尼系数\(c_2 \)的阻尼器与\(B_1\)联结. \(B_1 \)受简谐力\(F{\rm e}^{{\rm i}\omega t}\)的激励(图3).
列写此系统的动力学方程
\[{\pmb M}\ddot{\pmb x} + {\pmb C}\dot{\pmb x} + {\pmb K}{\pmb x} = {\pmb F}{\rm e}^{{\rm i}\omega t} \ \ (1)\]
各矩阵定义为
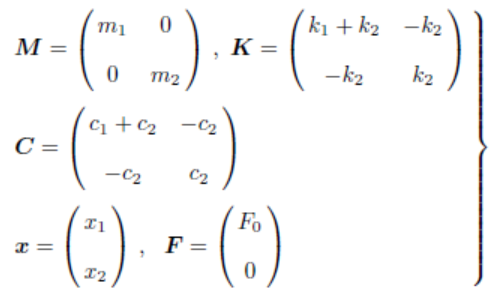 (2)
(2)
其中\(x_1 \), \(x_2 \)分别为\(B_1 \)和\(B_2 \)相对平衡位置的垂直位移. 令
\[{\pmb x} = {\pmb A}{\rm e}^{{\rm i}\omega t}, \ \ {\pmb A}= \left( {A_1 } \ \ {A_2 } \right)^{\rm T}\ \ (3)\]
代入方程(1), 化作
\[\left( {{\pmb K} - \omega ^2{\pmb M} + {\rm i}\omega {\pmb C}} \right) {\pmb A} = {\pmb F} \ \ (4)\]
解出
\[{\pmb A }= {\pmb H}{\pmb F} \ \ (5)\]
其中\({\pmb H} = \left( {{\pmb K} - \omega ^2{\pmb M}+ {\rm i}\omega {\pmb C}} \right)^{ - 1}\)为复频响应矩阵
\[{\pmb H} = \dfrac{1}{\varDelta \left( \omega \right)}\left(\!\! \begin{array}{c} {k_2 - m_2 \omega ^2 + {\rm i}\omega c_2 } \ \ \ \ {k_2 + {\rm i}\omega c_2 } \\ {k_2 + {\rm i}\omega c_2 } \ \ \ \ {k_1 + k_2 - m_1 \omega ^2 +{\rm i}\omega \left( {c_2 - c_1 } \right)}\end{array} \right) \ \ (6)\]
\[\varDelta \left( \omega \right) = \left| {{\pmb K} - \omega ^2{\pmb M} + {\rm i}\omega {\pmb C}} \right| = \left( {k_1 - m_1 \omega ^2} \right)\left( {k_2 - m_2 \omega ^2} \right) + \left( {c_1c_2 - k_2 m_2 } \right)\omega^2+\\ \qquad {\rm i}\omega \left\{ {c_2 \left[ {k_1 - \left( {m_1 + m_2 }\right)\omega ^2} \right] -}\right. \left. { c_1 \left( {k_2 - m_2 \omega ^2} \right)} \right\} \ \ (7)\]
从式(5)导出受迫振动的振幅
\[\left. A_1 = \dfrac{F_0 }{\varDelta \left( \omega \right)}\left( {k_2 - m_2 \omega ^2 + {\rm i}\omega c_2} \right) \\ A_2 = - \dfrac{F_0 }{\varDelta \left( \omega \right)}\left( {k_2 + {\rm i}\omega c_2 }\right) \!\!\right\} \ \ (8)\]
将\(B_1 \)的振幅\(A_1 \)写作
\[A_1 = \dfrac{F_0 }{D\left( \omega \right)}\left[ {P\left( \omega \right) +{\rm i}Q\left( \omega \right)} \right] \ \ (9)\]
其中\( P\left( \omega \right)\)等函数可表示为
\[\left.\begin{array}{l} P\left( \omega \right) = \left[ {\left( {k_1 - m_1 \omega ^2} \right)\left({k_2 - m_2 \omega ^2} \right) - }\right. \\ \left.{ k_2 m_2 \omega ^2} \right]\left( {k_2 - m_2\omega ^2} \right) +\\ \qquad c_{2}^2 \omega ^2\left[ {k_1 - \left( {m_1 + m_2 } \right)\omega ^2}\right]\\ Q\left( \omega \right) = \omega \Big [c_2 \omega ^2\left( {c_1 c_2 - m_2^2 \omega ^2} \right) - c_1 \left( {k_2 - m_2 \omega ^2} \right)^2\Big]\\ D\left( \omega \right) = \left[ {\left( {k_1 - m_1 \omega ^2} \right)\left( {k_2 - m_2 \omega ^2} \right)+}\right. \\ \qquad \left.{ \left( {c_1 c_2 - k_2 m_2 } \right)\omega ^2} \right]^2 -\\ \qquad\omega ^2\left\{ {c_2 \left[ {k_1 - \left( {m_1 + m_2 } \right)\omega ^2} \right] - }\right. \\ \qquad\left.{ c_1 \left( {k_2 - m_2 \omega ^2} \right)} \right\}^2 \end{array}\right\} \ \ (10) \]
为消除建筑物\(B_1 \)的振动, \(P\left( \omega \right)\)必须为零, 其充分条件为
\[k_2 - m_2 \omega ^2 = 0 \ \ (11a)\]
\[$k_1 - \left( {m_1 + m_2 } \right)\omega ^2 = 0\ \ (11b)\]
其中式(11a)是与无阻尼情形相同的消振条件, 即要求消振器\(B_2 \)的无阻尼固有频率\(\sqrt {{k_2 } /{m_2 }} \)等于激励频率. 式(11b)为有阻尼情形的附加条件, 要求\(\sqrt {{k_1 } /{\left( {m_1 + m_2 } \right)}}\)亦等于激励频率. 如\(m_1 \gg m_2 \), 此条件相当于\(B_1 \)的无阻尼固有频率\(\sqrt {{k_1 } /{m_1 }} \)接近激励频率.实际上即使在无阻尼情形, 如将建筑物的基频取作待消除的激励频率, 此条件亦自行满足.
但要实现完全消振, 条件(11)并不充分. 因为除\(P\left( \omega \right)\)为零以外, \(Q\left( \omega \right)\)也必须同时为零, 即要求\(c_1 c_2 - m_2^2 \omega ^2\)也为零. 但此条件因导致\(D\left( \omega \right) = 0\)而不可能满足, 否则将使\(A_1 \)成为不定值, \(A_2 \)的值成为无限大. 可见条件(11)仅是消振的必要条件, 即使满足, 建筑物仍有残余振动存在. \(B_1 \)和\(B_2 \)的受迫振动振幅分别为
\[\left. A_1 = \dfrac{{\rm i}c_2 F_0 }{\left( {c_1 c_2 - k_2 m_2 } \right)\omega } \\ A_2 \; = \dfrac{F_0 \left( {k_2 + {\rm i}c_2 \omega } \right)}{\left( {c_1c_2 - k_2 m_2 } \right)\omega ^2} \right\} \ \ (12)\]
如选择较小的消振器质量\(m_2 \)和刚度系数\(k_2 \), 较强的阻尼系数\(c_2 \), 且由于建筑物通常有足够强的阻尼, 导致\(c_1c_2 \gg k_2 m_2 \). 可将式(12)中的\(c_1 c_2 - k_2 m_2 \)近似以\(c_1 c_2 \)代替, 导出\(A_1 \)和 \(A_2 \)模的近似值
\[\left| {A_1 } \right| = \dfrac{F_0 }{c_1 \omega }, \ \ \left| {A_2 } \right| = \dfrac{F_0 }{c_1 \omega }\sqrt {1 + \left( {\dfrac{k_2}{c_2 \omega }} \right)^2} \ \ (13)\]
可见建筑物的振幅\(\left| {A_{1} } \right|\)取决于阻尼系数\(c_1\), 而消振器的振幅\(\left| {A_2 } \right|\)与刚度系数\(k_2 \)和阻尼系数\(c_2\)有关.
以上在线性振动范畴内所做的分析表明, 对于有阻尼的二自由度线性系统, 消振器的无阻尼固有频率等于激励频率的消振条件仍为消振的必要条件, 同时还要求建筑物的无阻尼固有频率亦接近激励频率. 但即使上述条件满足, 有阻尼系统也不能实现完全消振. 建筑物仍有残余振动存在, 其幅度与本身的阻尼系数\(c_1\)成反比. 消振器的振动幅度则可通过减小刚度系数\(k_2 \)和增大阻尼系数\(c_2\)进行调整.
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|