引用本文
李双, 刚宪约. 有限元模型阻尼特性的复参数修正方法研究. 力学实践, 2018,40(1): 45-50
LI Shuang, GANG Xianyue. A COMPLEX PARAMETER MODEL UPDATING METHOD FOR DAMPING CHARACTERISTICS OF FINITE ELEMENT MODELS. MECHANICS IN ENGINEERING, 2018,40(1): 45-50.  
Doi: 10.6052/1000-0879-17-207
Permissions
Copyright©2018, 力学所
有限元模型阻尼特性的复参数修正方法研究
李双1,2, 刚宪约1
1.山东理工大学 交通与车辆工程学院,山东 淄博 255049
2.联合汽车电子有限公司,上海 201206

作者简介：李双,硕士研究生.刚宪约, 副教授,研究方向为结构动力学. E-mail: gangxianyue@sdut.edu.cn

收稿日期: 2017-09-24
资助项目: 山东省自然科学基金 (ZR2014AL010),山东省重点研发计划(2015GGX105003)资助项目.
摘要

阻尼对于结构动力学响应具有重要的影响,但有限元模型一般很难对阻尼特性进行精确建模.基于实测频响函数,研究了一种有限元模型阻尼特性的复参数修正方法.以待修正区域各单元质量、刚度矩阵的比例修正系数为复修正参数,建立了单元矩阵比例修正的灵敏度方程直接算法,并对比分析了复修正参数与不同阻尼特性之间的数学关系.以六自由度集中参数模型和25杆平面桁架模型为例,验证了复参数修正方法在阻尼特性修正中的有效性.

关键词: 复参数; 阻尼特性; 频响函数; 模型修正
中图分类号:U461.1 文献标志码:A
A COMPLEX PARAMETER MODEL UPDATING METHOD FOR DAMPING CHARACTERISTICS OF FINITE ELEMENT MODELS
LI Shuang1,2, GANG Xianyue1
1.School of Transportation and Vehicle Engineering, Shandong University of Technology, Zibo 255049, Shandong, China
2.UAES, Shanghai 201206, China
Abstract

Damping plays an important role in structural dynamics. However,it is difficult to model the damping characteristics in the finite element analysis. Using the experimental and analytical frequency response functions (FRF), a complex parameter model updating method is developed to update the mass, stiffness and damping properties. Taking the complex proportional coefficients of the element matrices as the updating variables, the direct updating sensitivity equation system is deduced, and the relationship between the complex updating parameters and the typical damping types is revealed. At the end, the performance of the proposed method is evaluated with examples of a 6-DOF lumped system and a 25 truss structure.

Key words: complex parameters; damping characteristics; frequency response function; model updating

在工程实际中, 构建一个精确的有限元模型是进行结构有限元分析的基础. 然而在建立有限元模型时, 不可避免地存在各种理论假设、边界条件的近似性、材料参数的不确定性等因素, 使得有限元模型和实际模型之间存在误差. 为了改善这一问题, 对结构动力学模型修正方法进行研究就变得十分必要.

目前, 有限元模型修正方法已经广泛应用于机械工程、航空航天、建筑工程等领域. 根据修正过程中使用试验数据的不同, 现有的模型修正方法可以分为基于模态参数的模型修正方法[1]和基于频响函数的模型修正方法[2]两大类, 由于频响函数法回避了模态参数识别这个步骤, 在模型修正中积累的误差比模态参数法更少, 因此在近些年逐渐发展起来. 然而传统的模型修正方法修正的重点一般都是刚度和质量参数, 待修正的有限元模型不考虑或暂不考虑阻尼特性. 而实际结构中往往是存在阻尼的, 由于阻尼能够衰减结构系统的振动能量, 减小振动共振区内的振幅, 因此当忽略结构的阻尼时, 建立的有限元模型与实际结构会存在一定的偏差. 而且在修正计算中, 通常将实测有阻尼数据与有限元无阻尼仿真数据直接进行相关性分析来实现模型修正, 但由于阻尼所造成的频响函数零极点频移和峰值衰减都会给模型修正带来误差, 因此为了保证修正结果的准确性, 开展考虑阻尼特性的模型修正方法研究必不可少.

袁永新等[3, 4]利用实测复模态参数, 提出了一种基于奇异值分解的黏性阻尼矩阵直接修正方法.季佳[5]提出 了三种正交模态修正方法来解决黏性阻尼特性的修正方法.保宏等[6]基于Lin等[7]的频响函数直接修正方法, 引入阻尼刚度比来实现对阻尼特性的修正, 本质上属于对结构阻尼特性的修正. 本文就是将保宏等 的方法进行进一步推广, 研究一种适用于一般阻尼特性的复参数修正方法.

1 基于频响函数的模型修正方法

Lin等[7]于20世纪初提出了基于频响函数的模型修正方法, 其灵敏度修正方程为

\[ \left[ {\pmb S}_{\rm m} \left( \omega \right) \ \ {\pmb S}_{\rm c} \left( \omega \right) \ \ {\pmb S}_{\rm k} ( \omega ) \right]\left\{\begin{array} \!\! {\pmb p}_{\rm m} \\ {\pmb p}_{\rm c} \\ {\pmb p}_{\rm k} \end{array} \!\! \right\} = {\pmb h}_{\rm a} \left( \omega \right) -{\pmb h}_{\rm x} \left( \omega \right) \ \ (1)\]

式中, \({\pmb S}_{\rm m} \left( \omega \right)\), \({\pmb S}_{\rm c} \left( \omega \right)\)及\({\pmb S}_{\rm k} \left( \omega \right)\)为灵敏度矩阵, \({\pmb p}_{\rm m} \), \({\pmb p}_{\rm c} \)及\({\pmb p}_{\rm k} \)分别为与单元质量矩阵、单元阻尼矩阵和单元刚度矩阵相关的比例修正参数列向量

\[{\pmb S}_{\rm m} \left( \omega \right) = - \omega ^2\left[ {\pmb H}_{\rm a} {\pmb M}_{\rm 1}^{\rm e} {\pmb h}_{\rm x} \ \ {\pmb H}_{\rm a} {\pmb M}_{\rm 2}^{\rm e} {\pmb h}_{\rm x} \cdots {\pmb H}_{\rm a} {\pmb M}_{n_m }^{\rm e} {\pmb h}_{\rm x} \right]\]

\[{\pmb S}_{\rm c} \left( \omega \right) = {\rm j}\omega \left[{\pmb H}_{\rm a} {\pmb C}_{\rm 1}^{\rm e} {\pmb h}_{\rm x} \ \ {\pmb H}_{\rm a} {\pmb C}_{\rm 2}^{\rm e} {\pmb h}_{\rm x} \ \ \cdots \ \ {\pmb H}_{\rm a} {\pmb C}_{n_c }^{\rm e} {\pmb h}_{\rm x} \right] \]

\[{\pmb S}_{\rm k} \left( \omega \right) = \left[{\pmb H}_{\rm a} {\pmb K}_{\rm 1}^{\rm e} {\pmb h}_{\rm x} \ \ {\pmb H}_{\rm a} {\pmb K}_{\rm 2}^{\rm e} {\pmb h}_{\rm x} \ \ \cdots \ \ {\pmb H}_{\rm a} {\pmb K}_{n_k }^{\rm e} {\pmb h}_{\rm x} \right]\]

\({\pmb p}_{\rm m} = \left\{ p_{{\rm m}1} \ \ p_{{\rm m}2} \ \ \cdots \ \ p_{{\rm m}n_{\rm m} } \right\}^{\rm T}\)$

\[{\pmb p}_{\rm c} = \left\{ p_{{\rm c}1} \ \ p_{{\rm c}2} \ \ \cdots \ \ p_{{\rm c}n_{\rm c} } \right\}^{\rm T}\]

\[{\pmb p}_{\rm k} = \left\{p_{{\rm k}1} \ \ p_{{\rm k}2} \ \ \cdots \ \ p_{{\rm k}n_{\rm k} } \right\}^{\rm T}\]

式中, \({\pmb H}_{\rm a} \)及\({\pmb h}_{\rm x}\)分别表示频率点 \(\omega\)处的理论频响函数矩阵与试验频响函数列向量, 下标``a''及``x''分别表示理论与试验 模型; 下标\(n_{\rm m} \), \(n_{\rm c} \), \(n_{\rm k} \)分别代表待修正的单元质量矩阵、单元阻尼矩阵及单元刚度矩阵的个数; \(p_{{\rm m}i}\), \(p_{{\rm c}i}\)及\(p_{{\rm k}i}\)为待修正单元矩阵的比例修正系数, \({\pmb M}_i^{\rm e} \), \({\pmb C}_i^{\rm e} \)及\({\pmb K}_i^{\rm e} \)分别为第\(i\)个单元的质量矩阵、单元阻尼矩阵和单元刚度矩阵; \({\rm j}=\sqrt{-1}\).

一般情况下, 由于试验条件的限制或结构本身存在的不足, 通过实测结构上分布的测点通常无法获得修正过程所需的全部自由度的响应, 而测量转动自由度的响应则更加困难, 因此在得到的数据中, 实测结构的自由度数目远远小于有限元模型的自由度数目. 在一般的有限元模型修正算法中, 往往要求有限元模型的自由度与实测模型的自由度能够一一对应, 因此, 借鉴本文作者在文献[8]提出的基于非完备频响函数的模型修正新格式, 通过动态缩聚方法将理论模型进行缩聚. 最终可得缩聚模型的修正公式如下

\[{\pmb S}^{\rm R}{\pmb p} = {\pmb h}_{\rm a}^{\rm R} \left(\omega \right) - \tilde{\pmb h}_{\rm x} \left( \omega \right) \ \ (2)\]

式中, \({\pmb h}_{\rm a}^{\rm R} \left( \omega \right)\)为模型缩聚后的理论模型频响函数列向量; \(\tilde{\pmb h}_{\rm x} \left( \omega \right)\)为模型缩聚后经过修改的试验频响函数列向量

\[ \tilde{\pmb h}_{\rm x} \left( \omega \right) = {\pmb H}_{\rm a}^{\rm R} \left( \omega \right)\Big[ {\pmb T}_{\rm xd}^{\rm T} \left( \omega \right)\left( { - \omega ^2{\pmb M} + {\rm j}\omega {\pmb C} + }\right. \ \ \qquad \left. {{\pmb K}} \right){\pmb T}_{{\rm xd}} \left( \omega \right)\Big]{\pmb h}_{\rm x} \left( \omega \right) \]

其他各参数的表达式为

\[{\pmb p} = \left\{ {\pmb p}_{\rm m}^{\rm T} \ \ {\pmb p}_{\rm c}^{\rm T} \ \ {\pmb p}_{\rm k}^{\rm T} \right\}^{\rm T} = \left\{ p_{{\rm m}1} \ \cdots \ p_{{\rm c}1} \ \cdots \ p_{{\rm k}1} \ \cdots \right\}^{\rm T}\]

\[{\pmb S}^{\rm R} = \left[ {\pmb S}_{\rm m}^{\rm R} \left( \omega \right) \ \ {{\pmb S}_{\rm c}^{\rm R} \left( \omega \right)} \ \ {{\pmb S}_{\rm k}^{\rm R} \left( \omega \right)} \right] \]

\[{\pmb S}_{\rm m}^{\rm R} \left( \omega \right) = - \omega^2 \left[ {\pmb H}_{\rm a}^{\rm R} \left( \omega \right){\pmb T}_{\rm xd}^{\rm T} \left( \omega \right){\pmb M}_{\rm 1}^{\rm e} {\pmb T}_{\rm xd} \left( \omega \right){\pmb h}_{\rm x} \left( \omega \right) \ \cdots \ \right]\]

\[{\pmb S}_{\rm c}^{\rm R} \left( \omega \right) = {\rm j}\omega \left[ {\pmb H }_{\rm a}^{\rm R} \left( \omega \right){\pmb T }_{\rm xd}^{\rm T} \left( \omega \right){\pmb C }_{\rm 1}^{\rm e} {\pmb T}_{\rm xd} \left( \omega \right) {\pmb h}_{\rm x} \left( \omega \right) \ \ \cdots \ \ \right]\]

\[{\pmb S}_{\rm k}^{\rm R} \left( \omega \right) = \left[{\pmb H}_{\rm a}^{\rm R} \left( \omega \right){\pmb T}_{\rm xd}^{\rm T} \left( \omega \right){\pmb K}_{\rm 1}^{\rm e} {\pmb T}_{\rm xd}\left( \omega \right){\pmb h}_{\rm x} \left( \omega \right) \ \ \cdots \ \ \right]\]

其中, 上标``R''表示缩聚模型, \({\pmb H}_{\rm a}^{\rm R}\)表示缩聚后的理论模型的频响函数, \({\pmb T}_{\rm xd}\)是试验模型的动态缩聚转换矩阵.

2 阻尼特性的复参数修正方法

在基于频响函数的有限元模型修正方法的基础上, 研究考虑有限元模型阻尼特性的复参数修正方法. 其中无阻尼结构有限元理论模型的对应频响函数数据均为实数, 而有阻尼试验模型的对应频响函数数据均为复数.

在有限元理论模型中, 一般很难精确模拟单元的阻尼特性, 因此使用方程(1)进行模型的阻尼特性修正在实际中存在许多困难.在本文的模型修正过程中, 设实测结构具有阻尼特性, 将每个单元的阻尼矩阵表示为其质量矩阵和刚度矩阵的复系数线性叠加.从而将传统的单元质量矩阵、单元刚度矩阵的实系数比例修正发展为复系数修正[9]. 单元比例修正系数表示为

\[p^{\rm C} = p^{\rm R} + {\rm j}p^{\rm I} \ \ (3)\]

式中, 比例修正参数\(p^{\rm C}\)的实部\(p^{\rm R}\)表示结构单元质量和刚度矩阵改变的比例系数, 虚部\(p^{\rm I}\)用来描述与质量、刚度特性相关的结构模型的阻尼特性.

这种采用虚部比例系数描述结构阻尼特性的方法, 可以比较好地描述一般结构的结构阻尼或黏性阻尼特性. 仅仅讨论修正系数虚部描述阻尼特性的有效性, 可以将一般线性结构的运动微分方程表示如下

\[ \left[ {\sum {\left( {1 + \left( {p_{\rm M}^{\rm C} } \right)_{\rm e} } \right){\pmb M}_{\rm e} } }\right] \ddot {\pmb X} + \left[ {\sum {\left( {1 + \left( {p_{\rm K}^{\rm C} } \right)_{\rm e} } \right){\pmb K}_{\rm e} } } \right]{\pmb X} = {\pmb F} \ \ (4)\]式中, \({\pmb M}_{\rm e} \)和\({\pmb K}_{\rm e} \)为扩展到与结构自由度数同阶的单元质量矩阵和单元刚度矩阵, \(\left({p_{\rm M}^{\rm C} } \right)_{\rm e} \)和 \(\left( {p_{\rm K}^{\rm C} } \right)_{\rm e}\)为单元质量矩阵、单元刚度矩阵的比例修正系数, \({\pmb X}\)和\({\pmb F}\)为节点位移向量和激振力向量.

本文讨论的模型修正以频响函数为参考, 而频响函数定义为简谐输出与简谐输入的比值[10], 令\({\pmb F} = \bar{\pmb F}{\rm e}^{{\rm j}\omega t}\), \({\pmb X}= \bar{\pmb X}{\rm e}^{{\rm j}\omega t}\). 对于具有结构阻尼的系统, 其结构运动微分方程(4)变换可得

\[ \left[ {\sum {\left( {1 + \left( {p_{\rm M}^{\rm R} } \right)_{\rm e} }\right){\pmb M}_{\rm e} } } \right]\ddot{\pmb X} +{\rm j}\sum \left[ { - \omega ^{\rm 2}\left({p_{\rm M}^{\rm I} } \right)_{\rm e} {\pmb M}_{\rm e} + \left( {p_{\rm K}^{\rm I} } \right)_{\rm e} {\pmb K}_{\rm e} } \right] {\pmb X} + \left[ {\sum {\left( {1 + \left( {p_{\rm K}^{\rm R} } \right)_{\rm e} } \right){\pmb K}_{\rm e} } }\right]{\pmb X} = {\pmb F} \ \ (5)\]

若\(\left( {p_{\rm M}^{\rm I} } \right)_{\rm e} = 0\), 则式(5)描述的就是经典的结构阻尼模型. 对于具有黏性阻尼的系统, 由式(4)变换可得

$$ \left[ {\sum \left( {1 + \left( {p_{\rm M}^{\rm R} } \right)_{\rm e} }\right){\pmb M}_{\rm e} } \right]\ddot{\pmb X} +\sum \left[ {{\rm j}\omega \left( {p_{\rm M}^{\rm I} } \right)_{\rm e} {\pmb M}_{\rm e} + \dfrac{1}{{\rm j}\omega }\left( {p_{\rm K}^{\rm I} } \right)_{\rm e} {\pmb K}_{\rm e} } \right]\dot{\pmb X}+ \left[ {\sum \left( {1 + \left( {p_{\rm K}^{\rm R} } \right)_{\rm e} } \right){\pmb K}_{\rm e} }\right]{\pmb X} = {\pmb F} \ \ (6)$$

式(6)形式上表示成了黏性阻尼方程的形式, 但黏性阻尼矩阵与激励频率有关, 这一点与经典的黏性阻尼不同.

3 数值案例
3.1 集中参数模型

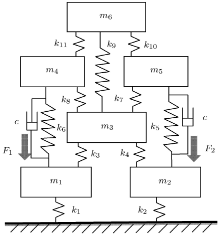
以如图1所示六自由度集中参数模型[11]为例, 对比验证本文研究的复参数修正方法对结构阻尼和黏性阻尼修正的有效性.

图1 六自由度集中参数模型

3.1.1 结构阻尼参数修正

不考虑图1中的黏性阻尼环节, 假定试验模型部分弹簧存在与其刚度参数成比例的结构阻尼, 理论模型没有考虑阻尼作用, 并且理论模型的部分质量、刚度参数与试验模型存在比例偏差.

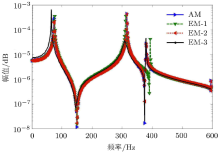
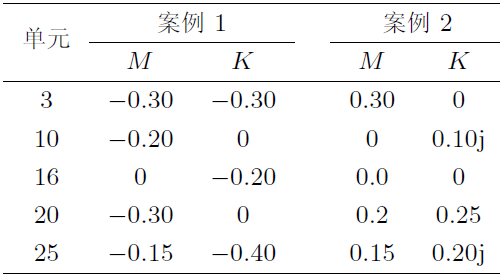
如表1所示, ``理论模型''表示待修正模型的参数, "案例1"、“ 案例2” 、“ 案例3” 分别代表3种存在不同的比例参数偏差的试验模型.理论模型与试验模型的\(H_{11} \)频响函数的对比如图2所示, 其中, 图例AM表示有限元理论模型, EM-1, EM-2, EM-3分别表示3种不同的试验模型案例.

表1 初始结构参数及不同修正案例

图2 理论模型与试验模型的\(H_{11} \)对比图

基于理论与试验频响函数数据, 利用复参数修正方法进行质量、阻尼和刚度参数联合修正所得结果如表2所示, 可以看出三组试验模型的修正结果与预设目标值完全一致.

表2 预设目标值与修正值

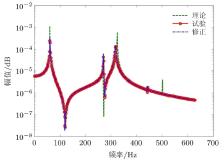
图3给出了3个案例修正模型与试验模型的频响函数\(H_{41}\)曲线, 可以看出修正模型与试验模型的频响函数数据吻合得非常好.

图3 修正模型和试验模型的\(H_{41}\)对比图

3.1.2 黏性阻尼参数修正

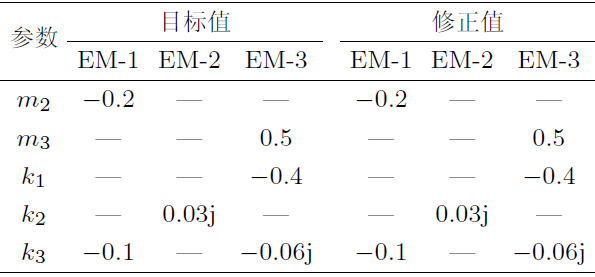
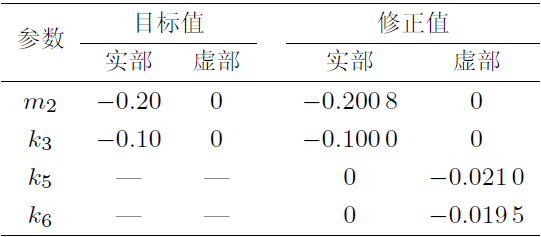
对于图1所示集中参数模型, 仍假定有限元理论模型未考虑阻尼作用, 而试验模型存在阻尼系数\(c=100 \)Ns/m的两个黏性阻尼环节. 为验证本文复参数修正方法对于黏性阻尼系统的质量、刚度和阻尼参数联合修正的能力, 同时预设理论模型的\(m_{2}\), \(k_{3}\)相对于试验模型存在0.2, 0.1的比例缩减系数.

采用复参数修正方法进行模型修正, 其结果如表3所示; 修正后的频响函数曲线与实测频响函数对比如图4所示, 模型修正后的频响函数曲线与实测频响函数曲线在整个频率范围内吻合得非常好. 结合上节对结构阻尼模型的修正结果, 可推知复参数修正方法对常见的结构阻尼和黏性阻尼都可以适用.

表3 预设目标值与修正值

图 4 修正模型对应的\(H_{11} \)对比图

3.2 分布参数模型

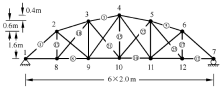
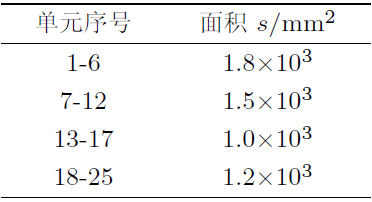
如图5所示25杆平面桁架结构[8], 材料杨氏模量为\(E = 200\) GPa, 泊松比为\(\nu =0.3\), 密度为\(\rho =7.8 \times 10^{3}\) kg/m\(^{3}\), 各杆的横截面积如表4所示.

图5 平面桁架模型

假定理论模型没有考虑阻尼作用, 而试验模型具有结构阻尼, 即某些杆件存在与其刚度成比例的阻尼, 同时仍假定理论模型的某些杆件相对于试验模型存在质量、刚度比例偏差. 预设的两个试验案例杆单元比例偏差系数如表5所示.

表4 杆单元的横截面积
表 5 部分杆单元的比例偏差系数

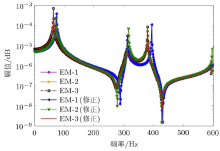
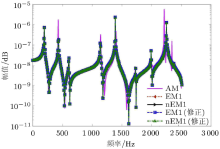
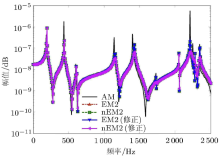
分别取理论频响函数与两个案例试验的频响函数数据, 利用灵敏度方程进行理论模型的修正. 图6和图7分别给出了两个案例的原始理论模型(AM)、无噪声试验模型(EM)、有噪声试验模型(nEM)、无噪声修正模型(EM(修正))、有噪声修正模型(nEM(修正))的\({ H}_{11} \)曲线图. 其中有噪声试验模型添加了2%的高斯白噪声.

分别对比有、无噪声干扰两种情况下的修正模型与试验模型的频响函数曲线, 可以看出无噪声干扰修正结果与对应的试验模型曲线完全重合, 受到噪声干扰的修正结果则与对应试验模型曲线也吻合得非常好. 由于案例1中并没有添加阻尼特性, 采用复参数修正方法进行模型修正, 也能得到正确可靠的修正结果, 因此可认为复参数修正方法对于无阻尼和有阻尼模型都是适用的.

图6 案例1试验模型及修正模型\(H_{11}\)对比图

图7 案例2试验模型及修正模型\(H_{11}\)对比图

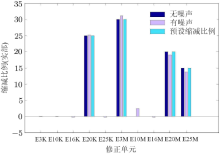
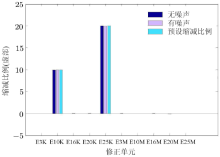
在图8和图9中分别给出了案例2比例参数修正结果的实部和虚部对比柱状图. 其中, 横轴上"E* K" 或"E* M"表示修正单元的刚度或质量, * 表示修正单元编号.

图8 案例2对应比例参数修正实部对比图

图9 案例2比例参数修正虚部对比图

观察上面两图可知, 噪声的干扰对比例参数的实部修正能够产生一定的影响, 但对虚部产生的作用不大. 由于修正比例参数的虚部代表结构模型的阻尼特性, 因此可推出, 复参数修正算法对存在噪声干扰的分布参数模型能够进行有效的阻尼参数修正.

4 结 论

实际结构的阻尼物理机理都非常复杂, 无论是结构阻尼、黏性阻尼、库伦阻尼或比例阻尼都只不过是在当前认知范围内, 为了分析方便对结构阻尼特性的一种抽象和简化. 只要是在较宽的频率范围对能量耗散特性的描述能够逼近实际实验数据, 都可以认为是好的模拟方式.

在基于频响函数的模型修正方法基础上发展而来的阻尼特性复参数修正方法, 可以很好地解决有限元模型的质量、刚度和阻尼联合修正问题, 从动力学方程分析和实例修正计算都验证了本文方法能够较好地模拟和修正一般的阻尼特性, 为改进有限元模型, 更精确地模拟结构的动态特性提供了一种切实可行的途径.

The authors have declared that no competing interests exist.

参考文献
[1] Hu SLJ, Li H, Wang S. Cross-model cross-mode method for model updating. Mechanical Systems and Signal Processing, 2007, 21(4): 1690-1703 [本文引用:1]
[2] 朱凼凼, 冯咬齐. 应用位移频响函数进行模型修正. 宇航学报, 2006, 27(2): 201-204 [本文引用:1]
[3] 袁永新, 戴华. 阻尼矩阵与刚度矩阵的一种直接修正方法. 振动与冲击, 2009, 28(8): 117-120+203 [本文引用:1]
[4] 蒋家尚, 袁永新. 基于复模态实验数据的黏性阻尼矩阵的修正. 振动与冲击, 2007, 26(5): 74-76, 80, 155 [本文引用:1]
[5] 季佳. 一种黏性阻尼系统的模型修正方法研究. [硕士论文]. 南京: 南京航空航天大学, 2014 [本文引用:1]
[6] 保宏, 赵冬竹, 王从思等. 利用频响函数对阻尼结构进行模型修正的方法. 应用力学学报, 2010, (1): 68-72, 224 [本文引用:1]
[7] Lin RM, Ewins DJ. Model updating using FRF data. The 15th International Seminar on Modal Analysis, 1990 [本文引用:2]
[8] Gang X, Chai S, Allemang RJ, et al. A new iterative model updating method using incomplete frequency response function data. Journal of Sound and Vibration, 2014, 333(9): 2443-2453 [本文引用:2]
[9] Arora V, Singh SP, Kundra TK. Damped model updating using complex updating parameters. Journal of Sound and Vibration, 2009, 320(1): 438-451 [本文引用:1]
[10] Meirovitch L. Fundamentals of Vibrations. New York: McGraw-Hill, 2001 [本文引用:1]
[11] Urgueira APV, Almeida RAB, Maia NMM. On the use of the transmissibility concept for the evaluation of frequency response functions. Mechanical Systems and Signal Processing, 2011, 25(3): 940-951 [本文引用:1]