以脉动流输流管为例,利用非线性模态技术和一种数值迭代法研究陀螺连续体的非线性参数振动响应问题. 通过谐波平衡法将系统非线性非自治控制方程转化为拟自治方程,并在状态空间上利用不变流形法构造系统的非线性模态. 以对应自治系统的解为初值,采用一种数值迭代法来求解拟自治控制方程的模态系数,结果证明了该迭代法的快速收敛性. 在频域分析中得到了幅频响应和相空间上的不变流形,而在时域复模态分析中则发现了参激陀螺系统的正交相位差和行波振动现象.
The nonlinear normal mode technique and a numerical iterative approach are applied to study the nonlinear parametric vibrations of pipes conveying pulsating fluid as an example of gyroscopic continua. The nonlinear non-autonomous governing equations are transformed into a set of pseudo-autonomous ones by employing the harmonic balance method. The nonlinear normal modes are constructed by the invariant manifold method in the state space and a numerical iterative approach is adopted to obtain the modal coefficients, in which the modal solutions of the corresponding autonomous system are taken as the initial values. The results obtained see a fast convergence. The frequency-amplitude responses and the invariant manifolds are both obtained in the frequency-domain study, while the quadrature phase difference and the traveling waves are found in the time-domain complex modal analysis.
陀螺系统作为一种基础的工程结构, 在航空航天、国防军事、石油化工、机械自动化以及微纳机电等领域有广泛的应用.常见的陀螺系统分为两大类, 一类是轴向运动结构, 例如轴向运动梁、板和输流管道, 其陀螺效应来自于同向横向振动模态的陀螺耦合; 另一类是旋转结构, 其中, 绕自身轴线旋转体, 如一般传动轴, 其陀螺效应来自于异向横向振动的陀螺耦合, 而绕空间任意轴旋转体, 如发动机叶片等, 其陀螺效应则来自于轴向振动与横向振动的陀螺耦合.此外, 像钻柱等构件, 两类陀螺效应会同时产生, 属于双陀螺结构.
不论是否存在模态耦合, 非陀螺系统的振动问题都可以使用模态分析的方法进行研究.然而对于一个陀螺系统, 常常需要借助复模态来分析其动力学本质, 这就使模态分析变得复杂起来[1].众所周知, 在经典的实模态分析中, 如果给定任一自由度的位移/速度, 则其他所有自由度的位移/速度都可以表示为给定自由度位移/速度的函数.这说明所有自由度的位移或速度都保持同相位或相位差为\(\pi \), 也就是通常所说的"同步振动".然而在复模态分析中, 给定自由度的位移和速度都将出现在其他自由度位移或速度函数中.于是各个自由度之间可能出现各种相位差, 也就导致了所谓的"非同步振动".由于模态分析的主要意义是在线性范围内对机械系统进行分析设计, 对于复模态的研究也长期停留在线性范围内[2].直到近些年, 随着非线性模态理论的深入发展, 非线性复模态[3, 4]逐渐被采纳和使用, 从而将传统线性复模态理论拓展到非线性领域, 这也给非线性系统模态分析技术的发展提供了新的契机.
作为一类典型的陀螺系统, 输流管已经在各工程领域得到广泛应用.由于吸收了流体的动能, 管道常常发生自激振动, 这类振动对机械结构的破坏或潜在危害是巨大的.同时, 作为一类"典型的动力学问题", 输流管振动又具有相当重要的理论研究价值, 包括其线性和非线性振动, 以及自由振动、参数激励和外激励等多种形式的振动问题, 已成为工程界和学术界共同关注的热点.输流管振动问题早在19世纪就引起了人们极大的兴趣.Pa\"idoussis[5]在之后的著作中全面论述了柔性结构与轴向流的耦合作用机理.徐鉴等[6]总结了输流管非线性动力学研究的早期进展. Chen等[7]分析了输流管超临界振动问题.王琳等[8]则将研究拓展到微纳米领域, 阐述了尺度效应对输流管动力学行为的影响.实际上, 输流管在动力学本质上与轴向运动体类似, 区别仅在于轴向运动体本身沿轴向运动, 周围介质静止; 而输流管本身静止, 内部流体介质沿轴向运动.
陀螺结构的参数振动是一类重要的动力学行为.尽管对陀螺连续体的研究已取得了很多成果, 但就作者所知, 还未发现完全从模态分析的角度对陀螺系统的参激振动进行研究的相关报道.本文则以脉动流输流管为例, 研究参激陀螺系统的非线性响应问题.应用Shaw等[9]提出的不变流形法构造系统的非线性模态, 并利用一种有效的数值迭代法获取模态系数.通过频域分析和时域复模态分析对陀螺连续体的参数振动问题进行深入探讨.
当流体以一定相对速度穿过中空圆柱体时, 由于流固耦合作用会产生科氏力. 这是陀螺效应在平动弹性体上的典型体现.本文中将以两端固定脉动流输流管为例来研究这类陀螺系统的非线性参数振动响应问题.假定管道未变形轴线沿\(x\)轴方向, 且管道只发生横向面内振动\(y(x, t)\), \(t\)为时间变量. \(U\)表示管内流速.考虑中线伸长引起的几何非线性, 我们可以得到该陀螺系统的横向振动控制方程[10]
\[EI\dfrac{\partial ^4y}{\partial x^4} + M\left[ {U^2 + \dfrac{\partial U}{\partial t}\left( {L- x} \right)} \right]\dfrac{\partial ^2y}{\partial x^2} + (M + m)\dfrac{\partial ^2y}{\partial t^2} + \\ 2MU\dfrac{\partial ^2y}{\partial x\partial t} - \left[ {\dfrac{EA_p }{2L}\int_0^L{\left( {\dfrac{\partial y}{\partial x}} \right)^2} d x} \right]\dfrac{\partial ^2y}{\partial x^2} = 0\ \ (1)\]
式中\(E\), \(I\), \(L\), \(A_{p}\)和\(m\)分别表示管道杨氏模量、截面惯性矩、长度、横截面积和单位长度的质量, \(M\)表示流体单位长度的质量.引入无量纲变量和参数
\[\left.\begin{array}\quad \eta = \dfrac{y}{L} , \xi = \dfrac{x}{L} , \quad \tau = \left( {\dfrac{EI}{M+ m}} \right)^{\tfrac{1}{2}}\dfrac{t}{L^2} \\ M_r = \left( {\dfrac{M}{M + m}} \right)^{\tfrac{1}{2}}, \quad u = \left({\dfrac{M}{EI}} \right)^{\tfrac{1}{2}}LU \gamma = \dfrac{A_p L^2}{2I} \end{array}\!\!\right\} \ \ (2)\]
并设无量纲脉动流速为\[u = u_0 \left[ {1 + \mu \cos (2\omega \tau )} \right] \ \ (3)\]
式中\(u_{0}\)为平均流速, \(\mu \)和\(2 \omega \)为脉动幅值(假定很小)和频率. 将式 (2) 和式 (3) 代入式 (1)中可得到如下无量纲脉动流管道控制方程
\[ \dfrac{\partial ^4\eta }{\partial \xi ^4} + u_0^2 \dfrac{\partial ^2\eta }{\partial \xi ^2} +\dfrac{\partial ^2\eta }{\partial \tau ^2} + 2M_r u_0 \dfrac{\partial ^2\eta }{\partial \xi \partial \tau } =\]\[ \mu \left[ {2M_r u_0 \omega (1 - \xi )\sin (2\omega \tau )\dfrac{\partial ^2\eta}{\partial \xi ^2} - } \right.\left. { 2\cos (2\omega \tau )\left( {u_0^2 \dfrac{\partial ^2\eta }{\partial \xi^2} + M_r u_0 \dfrac{\partial ^2\eta }{\partial \xi \partial \tau }} \right)} \right] +\]\[ \left[ {\gamma \int_{ 0}^{ 1} {\left( {\dfrac{\partial \eta }{\partial \xi }}\right)^2 d\xi } } \right]\dfrac{\partial ^2\eta }{\partial \xi ^2} \ \ (4)\]
注意到上式中已忽略了 \(\mu \) 的高阶项.
为了构造系统的非线性模态, 首先利用2振型Galerkin法\[\eta (\xi , \tau ) = \sum_{i = 1}^2 {\psi _i (\xi )q_i (\tau )} \ \ (5)\]对偏微分方程进行截断. 式中 \(\psi_{i }\)(\(\xi \)) 和\(q_{i }\)(\(\tau \)) 为第\(i\)阶两端固定静态梁的模态函数和广义坐标. 一些文献[11, 12]已经指出, 对于输流管参数振动问题, 取2阶Galerkin离散已经可以得到比较精确的结果, 而相应的理论分析和实验结果在定性上也吻合得很好.因此本文中截断阶数取为2.此外, 由于管道本身属于细长弹性体, 而当其内部充满液体后, 整个结构更加接近于梁结构, 因此选取相应边界条件下梁的模态函数来模拟输流管的振型函数通常会得到比较理想的结果.目前大多数关于输流管动力学的研究也都采用梁模态来模拟输流管的振动模态\(^{[5\hbox{-}8]}\). 将式 (5) 代入式 (4)并利用振型的正交性, 可以得到二元二次常微分方程组
\[ \ddot {q}_1 - \beta \Big[ 1 + \mu \cos (2\omega \tau ) \Big]\dot {q}_2 + \ \ \Big[ k_1 - \dfrac{1}{2b}c_{11} \mu \beta \omega \sin (2\omega \tau ) + \ \ 2c_{11} \mu u_0^2 \cos(2\omega \tau )\Big ]q_1 + \\ \dfrac{1}{b}(b + e)\mu \beta \omega \sin (2\omega \tau )q_2 + \ \ n_{11} q_1^3 + n_{12} q_1 q_2^2 = 0 \ \ (6{\rm a}) \]
\[ \ddot {q}_2 + \beta \Big[ 1 + \mu \cos (2\omega \tau )\Big]\dot {q}_1 +\ \ \Big[ k_2 - \dfrac{1}{2b}c_{22} \mu \beta \omega \sin (2\omega \tau ) + \ \ 2c_{22} \mu u_0^2 \cos(2\omega \tau )\Big]q_2 +\\ \dfrac{1}{b}(e - b)\mu \beta \omega \sin (2\omega \tau )q_1 + \ \ n_{21} q_2 q_1^2 + n_{22} q_2^3 = 0 \ \ (6{\rm b})\]
式中
\[\begin{array}{l} \beta = 2M_r u_0 b , \ \ k_1 = u_0^2 c_{11} + \lambda _1^4 , \ \ k_2 =u_0^2 c_{22} + \lambda _2^4 \\ n_{11} = \gamma c_{11}^2 , \quad n_{12} = \gamma c_{11} c_{22} , \quad n_{21}= n_{12} \\ n_{22} = \gamma c_{22}^2 , \ \ b = 3.342 0 , \quad e = 3.342 6\\ c_{11} = - 12.302 6 , \ \ c_{22} = - 46.0501\ \\ \lambda _1 = 4.730 0 , \quad \lambda _2 = 7.8532 \end{array}\]
下面将利用不变流形法构造陀螺系统的非线性模态, 并利用数值迭代法[13]获取参数振动响应的模态系数.该迭代法将传统Rauscher法与非线性模态方法相结合, 具有较高的计算效率.为了有效实施迭代, 需要选取一组合适的模态系数值作为迭代初值.这里考虑原参激系统对应的自治系统, 通过不变流形法获得其非线性模态系数作为迭代初值. 令
\[\left[ {p_1 , \; p_2 } \right] = \left[ {\dot {q}_1 , \; \dot {q}_2 } \right] \ \ (7)\]
并设 \(\mu =0\), 则方程 (6) 可化为控制管道自由振动的一阶状态方程\[\left.\begin{array}{l} \dot {q}_1 = p_1 \ \ \dot {p}_1 = f_1 (q_1 , q_2 ; p_1 , p_2 ) =\ \ \beta p_2 - k_1 q_1 - n_{11} q_1^3 - n_{12} q_1 q_2^2 \ \dot {q}_2 =\\ p_2 \dot {p}_2 = f_2 (q_1 , q_2 ; p_1 , p_2 ) =\ \ - \beta p_1 - k_2 q_2 - n_{21} q_2 q_1^2 - n_{22} q_2^3 \end{array}\!\! \right\} \ \ (8)\]
考虑到系统 (8) 的陀螺耦合以及只含有三次非线性项, 可以在纯模态空间上将\(q_{1}\), \(p_{1}\), \(q_{2}\)和\(p_{2}\)间的非线性关系表示为
\[\left. q_1 = w , \quad p_1 = v \ \ q_2 = a_1 w + a_2 v + a_3 w^3 + a_4 w^2v + a_5 wv^2 + a_6 v^3\ \ p_2 = b_1 w + b_2 v + b_3 w^3 + b_4 w^2v + b_5 wv^2 + b_6 v^3 \!\! \right\} \ \ (9)\]
将式 (9) 后两式对时间求导, 并将式 (8) 和式 (9) 代入其中, 通过比较\(w\), \(v\), \(w^{3}\), \(w^{2}v\), \(wv^{2}\)和\(v^{3}\)项的系数可得到关于常系数\(a_{j}\)和\(b_{j}\), \(j=1, 2, \cdots, 6 \)的非线性代数方程组
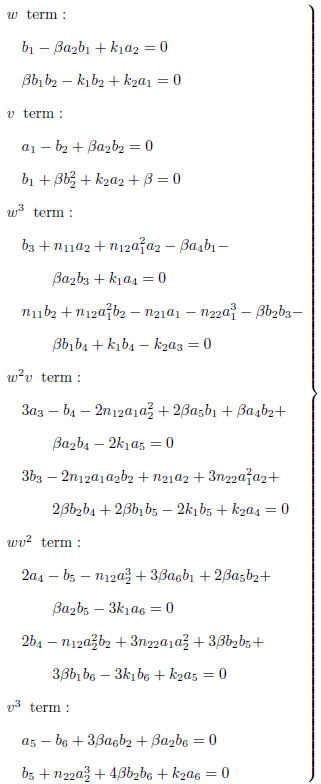
通过方程组 (10) 可求出未知模态系数, 这样就确定了迭代初值. 再考虑原非自治系统 (6), 将式 (9) 后两式带回系统 (6)的第一个方程可得到只关于\(q_{1}\)的非自治微分方程. 为了将其转化为自治方程, 假定其具有如下形式的周期解\[q_1 = A_1 \cos (\omega \tau ) + B_1 \sin (\omega \tau ) \ \ (11)\]
式中\(A_{1}\)和\(B_{1}\)可通过谐波平衡法求得. 利用式 (11) 可得如下表达式\[\left.\!\!\begin{array}{l} \cos (2\omega \tau ) = \alpha _1 q_1^2 + \alpha _2 \dot {q}_1^2 + \alpha _3q_1 \dot {q}_1 \ \ \sin (2\omega \tau ) = \dfrac{\omega \alpha _3 }{2}q_1^2 - \dfrac{\alpha _3}{2\omega }\dot {q}_1^2 + 2\omega \alpha _2 q_1 \dot {q}_1 \end{array}\!\!\right\} \ \ (12)\]
式中
\[\left. \alpha _1 = \dfrac{A_1^2 - B_1^2 }{\left( {A_1^2 + B_1^2 } \right)^2} \ \alpha _2 = \dfrac{B_1^2 - A_1^2 }{\omega ^2\left( {A_1^2 + B_1^2 } \right)^2}\ \ \alpha _3 = \dfrac{4A_1 B_1 }{\omega \left( {A_1^2 + B_1^2 } \right)^2}\!\!\right\} \ \ (13)\]
将式 (12) 代回式 (6) 即可得到近似的拟自治系统. 由于该系统仍然只含有三次非线性项, 在使用不变流形法时仍可采用式(9) 中的关系. 于是重复步骤 (7) \(\sim \) (10), 即可获得第一次迭代结果. 以该结果作为初值则可进行下一次迭代.
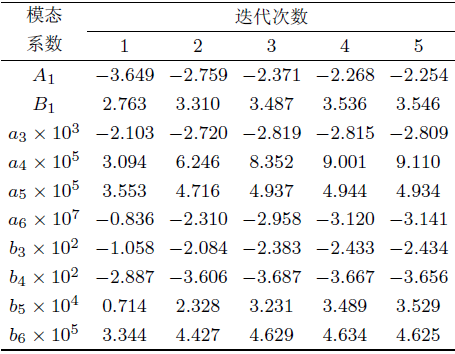
本节将通过数值算例分析陀螺系统第一阶主参数共振响应. 首先验证本文迭代法的收敛性. 算例中的参数值如下:\(u_{0}=3\), \(M_{r} = 0.8\), \(\omega = 22\), \(\mu = 0.3\), \(\gamma = 0.1\). 表1列出来前5次迭代结果.可以看出, 4次迭代就可以得到很高精度的结果了. 这证明了该迭代法的高效性, 同时说明了所选初值的合理性.
| 表1 由本文迭代法得到的模态系数值 |
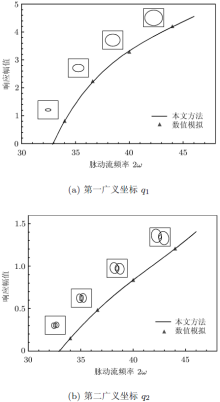
下面对本文参激陀螺系统进行频域分析.图1给出了利用前述非线性模态技术和迭代法得到的两个广义坐标\(q_{1}\)和\(q_{2}\)的非线性幅频 响应曲线, 以及由方程(6)直接数值模拟得到的结果以作比较. 可以看出, 两种方法所得结果相当吻合, 证明了本文方法的可靠性.同时, 在得到非线性模态系数值后, 还可以描绘出随着脉动频率的变化, 两个广义坐标在相空间上的演化, 如图1中所示.\(q_{1}\)的模态运动为简谐运动, 而\(q_{2}\)的模态运动则呈现明显的非线性特性. 因为由式 (11) 和式 (9)可以看出, \(q_{1}\)和\(p_{1}\)只含有基谐波, 而\(q_{2}\)和\(p_{2}\)则是\(q_{1}\)和\(p_{1}\)的复杂非线性函数.这也是利用不变流形法构造非线性模态的特点. 此外, 尽管\(q_{1}\)和\(q_{2}\)的响应曲线都表现出硬特性, 但从图1(a)和图1(b)的对比可以看出, 两个曲线的量值和走势还是有明显的不同. 这也是由上述原因所造成.
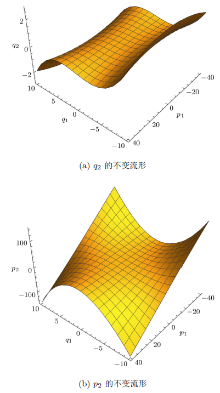
图2给出了参激陀螺系统的不变流形. 由于非线性的影响, 系统的不变流形不再保持平面.\(q_{2}\)的不变流形呈波浪形, 而\(p_{2}\)的不变流形则为翘曲面.从物理意义上讲, 不变流形的``不变性''是指任何起始于流形上的模态运动将会一直保持在该流形上, 而系统模态特性也将类似于流形上的一个非线性单自由度系统.对于本文所研究的参激陀螺系统, 我们可以得到类似于图1中的相空间上不同的模态运动周期轨道, 而所有可能的关于\(q_{2}\), \(q_{1}\), \(p_{1}\)和\(p_{2}\), \(q_{1}\), \(p_{1}\)的三维周期轨道则构成了图2中的非线性不变流形.
下面 利用非线性复模态法来分析系统的时域响应特性. 根据式 (11), 我们首先将\(q_{1}\)的周期解表示为复数形式
\[q_1 = A{\rm e}^{{\rm i}\omega \tau } \ \ (14)\]
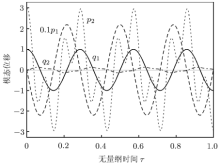
将式 (14) 代入式 (9) 中, 则\(p_{1}\), \(q_{2}\)和\(p_{2}\)均可表示为复数形式.为了分析两个广义坐标的相位关系, 给出系统发生参数振动过 程中\(q_{1}\), \(p_{1}\), \(q_{2}\)和\(p_{2}\)的时间历程图, 如图3所示. 图3和下面图4中的参数值均取:\(A = 1\), \(\omega = 22\).从图3中可以发现, \(q_{1}\)和\(q_{2}\)间存在\(\pi /2\)相位差, 即正交相位差, 而\(p_{1}\)和\(q_{2}\), \(p_{2}\)和\(q_{1}\)间相位差为\(\pi \)或同相位. 这是陀螺系统的典型特点.总的来说, 第二广义坐标的速度/位移总是和第一广义坐标的位移/速度相关, 这将导致陀螺系统出现非同步振动现象(图4(a)).
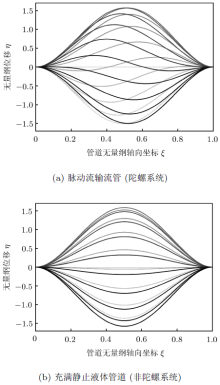
为了更清晰地展示复陀螺模态现象, 将复数形式的广义坐标和速度\(q_{1}\), \(p_{1}\), \(q_{2}\)和\(p_{2}\)代入式(5) 中, 可得 到系统在物理坐标上的振动响应.图4(a)和图4(b)分别给出了脉动流输流管和充满静止液体管道(非陀螺系统)一个周期内参数振动过程的快照.两图中曲线颜色由浅到深表示时间进行的方向.从图中可以清楚地看出, 非陀螺系统只存在固定的振动节点, 即只发生驻波形式的振动; 而对于陀螺系统, 由于前述正交相位差的存在, 振动节点将随时间发生移动, 表明系统此时发生的是行波形式的振动.而且对于第一阶主参数共振, 行波向左传播, 而管道中流体流动方向向右.正交相位差和行波现象是陀螺与非陀螺系统动力学行为上的重要区别.
本文以脉动流输流管为例, 从模态的角度研究了陀螺连续体的非线性参数振动响应问题.应用不变流形法构造了系统的非线性模态, 并利用一种数值迭代法获得了模态系数解. 文中得到的重要结论如下:
(1) 通过数值算例证明本文迭代法具有快速收敛性, 同时证明选取对应自治系统的模态系数为迭代初值是合理有效的.
(2) 尽管两个广义坐标的频域响应曲线都表现出硬特性, 但二者的量值和走势有明显的不同.尤其是第二广义坐标的模态运动呈现出明显的非线性特性.
(3) 由于非线性的影响, 系统的不变流形不再保持平面.第二广义坐标的不变流形呈波浪形, 而其对应速度的不变流形则为翘曲面.
(4) 在时域复模态分析中发现两个广义坐标间存在正交相位差, 导致参激陀螺系统出现非同步振动, 即行波振动现象.
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|