作者简介:刘宇飞,工学博士,研究方向为结构振动与损伤识别. E-mail:yufliu@gmail.com
为研究平稳随机振动下的结构响应估计与结构控制,首先对理想白噪声、限宽白噪声、连续限宽白噪声这三种白噪声模型的统计特征进行研究,对理想白噪声与限宽白噪声模型的时频特征进行了详细的理论分析,推导了连续限宽白噪声模型的自相关函数,并结合数值仿真对其信号频谱特征进行了验证与说明;其次,以三层剪切框架为例,详细推导了利用李雅普诺夫方程与理想白噪声模型预测结构振动信号的方差特性的过程;最后,针对广州新电视塔,利用随机地震金井清模型进行结构控制优化研究与分析,提出了同时考虑调频质量阻尼器频率与阻尼的结构控制优化设计方法.
For the structural response estimation and the control optimization under the stationary stochastic excitation, the statistical characteristics of the ideal white noise model, the band limited white noise model, and the continuous band limited white noise model are analyzed, especially the time-frequency characteristics of the ideal white noise model and the band limited white noise model. The self-correlation function of the continuous band limited white noise is derived, while its time-frequency characteristics are obtained based on the theoretical analysis together with numerical simulations. A three-story sheer frame is taken as an example, the variances of the vibration signals are predicted using the Lyapunov equation as well as the ideal white noise model. The TMD (tuned mass damper) system of the Guangzhou new TV tower is studied to illustrate the usage of the random vibration method in the structural control, and an optimization method is proposed with consideration of the frequency and the damping of the TMD system at the same time.
振动信号中的白噪声模型包括理想白噪声模型与限宽白噪声模型.白噪声模型的功率谱密度函数在整个频域或部分带宽内为恒值. 利用该特征, 白噪声模型在振动信号中有较多应用.在结构振动分析与振动信号处理中, 白噪声模型可作为实验噪声模型进行噪声的简化模拟[1, 2], 也可作为最简单的平稳激励来模拟环境激励下的载荷作用[3, 4].在白噪声的产生与使用中, 目前存在一些不合理的地方, 包括白噪声水平设置、带宽控制以及模型应用等多方面.本文对理想白噪声模型与限宽白噪声模型进行详细讨论.针对理想白噪声模型, 主要分析其时频特征以及在结构随机振动响应统计特征中的预测; 针对限宽白噪声模型, 对离散信号与连续信号两方面展开研究, 并对信号的时频特征进行了详细展示.以三层剪切框架为例, 推导并讨论了利用李雅普诺夫方程及理想白噪声模型对结构振动响应的方差进行预测的方法.同时结合广州新电视塔, 对使用随机振动方法进行结构调频质量阻尼器系统参数优化研究进行了探讨.
理想白噪声模型由美国Housner[5]于1947年提出, 用于对地震时的地面运动进行描述. 理想白噪声模型是无法用于仿真模拟的, 一般仅用于理论推导. 理想白噪声的定义为:功率谱密度函数在\(- \infty < \omega < + \infty \)为某常数, 其中\(\omega \)为频域横坐标. 注意其定义是从功率谱密度为恒值出发的, 而并非定义其分布. 理想白噪声有如下性质:
(1) 期望为零, 即零均值;
(2) 单位功率谱密度的白噪声, 自相关函数为克罗内克可函数.
对于白噪声\(X(T)\)有\(E[X(t)] \)等于0, 故:
(1) 其均方值\(E(X^2)\) 等于方差\(\sigma _X^2 \);
(2) 其自相关函数\(R_{XX} (\tau )\)等于自协方差函数\(C_{XX} (\tau )\).其中自相关函数、自协方差函数仅与\(\tau \)有关, 这是因为白噪声信号是平稳的.
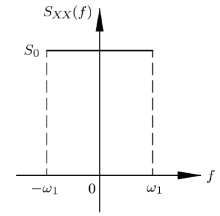
\(X(T)\)的双边功率谱密度函数(two-sided power spectral density)在\( - \infty < \omega < + \infty\)为常数, 设为\(S_0 \). 下面利用\(S_0 \)推导白噪声的统计参数:
根据维纳-辛钦(Wiener-\(\!\)-Khintchine)公式, \(X(T)\)的自相关函数\(R_{XX} (\tau)\)与功率谱密度函数\(S_X (\omega )\)为一傅氏对\[ R_{XX} (\tau ) = E[f(t)f(t + \tau )] = \int _{ - \infty }^{ + \infty }{S(\omega )} {\rm e}^{{\rm i}\omega \tau }d\omega = \int_{ - \infty }^{ + \infty } {S_0 } {\rm e}^{{\rm i}\omega \tau }d\omega = 2\pi S_0 \delta (\tau ) \ \ (1)\]
式中\(\delta (\tau )\)为狄拉克\(\delta \)函数. 由式(1)可见, 当\(\tau = 0\)时\(R_{XX} (\tau ) \to + \infty \), 当\(\tau\ne 0\)时\(R_{XX} (\tau ) = 0\). 即:\(\tau = 0\)时信号自相关, \(\tau \ne 0\)时的任何情况下信号均不自相关.
\(X(T)\)的方差\(\sigma _X^2 \)满足
\[\sigma _X^2 = \int_{ - \infty }^{ + \infty } {S_X } (\omega )d\omega =\int_{ - \infty }^{ + \infty } {S_0 } d\omega \to + \infty \ \ (2)\]或由\(\sigma _X^2 = R_{XX} (0)\)可知\[\sigma _X^2 = 2\pi S_0 \delta (0) \to + \infty \ \ (3)\]
因此在理想白噪声模型中, 讨论信号的方差/均方值, 或自相关函数/自协方差函数是没有意义的, 物理并中不存在这样的过程[6]. 实际白噪声的模拟中, 一般使用限宽白噪声来代替理想白噪声.在频域, 限宽白噪声的功率谱密度在有效带宽范围内 基本符合均匀分布.
限宽白噪声或带限白噪声(band limited white noise, BLWN)是指在一定频域范围内满足功率谱密度恒定的信号. 由于理想白噪声仅为理论模型、现实无法模拟, 在数值仿真中通常 用于模拟白噪声, 可用于连续或混合系统. 限宽白噪声的自相关函数与功率谱密度函数分别见图1与图2. 限宽白噪声可由多 种方式生成, 较多使用的是由满足高斯分布\(N(0, \sigma_X^2 )\)的随机信号生成. 对信号带宽的控制, 有两种方法:(1)利用 白噪声信号的采样频率来控制; (2)在生成较大带宽的白噪声后, 利用低通滤波器来控制其带宽. 应该注意的是, 生成的限宽 白噪声, 无法达到图2所示的功率谱密度函数理想的带宽边缘, 而是在带宽边界渐变. 在限宽白噪声的具体使用中, 需要对信号的带宽与幅值进行控制, 下面对二者逐一进行讨论.
1.2.1 限宽白噪声的幅值
当限宽白噪声作为噪声加入振动信号时, 一般通过信噪比来设置限宽白噪声的相对水平; 当作为振动激励信号时, 一般直接通过设置限宽白噪声的方差来调整其幅值大小. 信噪比(signal-to-noise ratio, SNR)表示的是期望信号与背景噪声的功率比例, 体现的是白噪声的相对水平[7]. 通常使用的信噪比是对数形式的, 单位为分贝(dB), 其表达形式见式(4), 其中\(P_{\rm Signal} \)为期望信号的功率, \(P_{\rm Noise} \)为背景噪声的功率, \(SNR_{\rm dB} \)为对数形式的信噪比.
\[SNR_{\rm dB} = 10\lg \Big(\dfrac{P_{\rm Signal} }{P_{\rm Noise} } \Big ) \ \ (4)\]
对于产生的高斯随机信号\(W\sim N (0, \sigma _X^2 )\), 方差为\(\sigma^2\), 信号的采样(间隔)时间\(\Delta t = {1}/f_{\rm s}\), 其中\(f_{\rm s}\)为采样频率(单位: s\(^{-1}\)), 则生成的限宽白噪声的功率谱密度为\(S_0 = {\Delta t\sigma ^2}/(2\pi )\).限宽白噪声的功率可由功率谱密度在频域积分得到, 从而可利用信噪比确定其相对水平.
1.2.2 限宽白噪声的带宽
本小节主要对利用随机数产生白噪声信号的方法进行讨论, 其带宽由信号的采样频率控制. 设白噪声的采样频 率为\(f_{s} \) (单位: s\(^{-1}\)), 采样(间隔)时间\(\Delta t = {1}/{f_{\rm s} }\), 则双边谱白噪声有效频域为\(f \in [ - f_{\rm s} /2, f_{\rm s}/2 ]\), 单边谱\(f \in [0, f_{\rm s}/2 ]\). 注意为使能量守恒, 单边功率谱密度为双边谱的两倍.在结构振动试验中因仅关心非负频率, 一般使用单边谱.
对高斯白噪声信号进行频域转换, 双边频域的最大范围为\({f_{\rm s} }/{2}\)(单位s\(^{- 1}\)), 无法观察频谱图中白噪声的带宽变化. 限宽白噪声的功率谱与采样频率之间的关系, 可以通过连续分布的矩形高斯白噪声近似得到, 具体内容将在第3节中进行阐述.
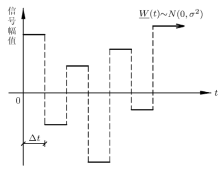
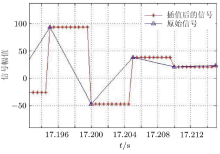
白噪声对试验结构进行激励时 给振动台输出的限宽白噪声 是 分段光滑的(见图3), 原因在于:数字模拟转换器 (digital-to-analog converter, DAC)的输出电压在达到信号的某个点后, 会在该水平上维持一个采样时间, 然后迅速 变化为下一个信号点水平. 因此要精确模拟振动台的行为, 需要使用连续限宽白噪声模型(见图3). 另一方面, 当对连续 时间系统的振动进行数值仿真时, 需要对离散的限宽白噪声信号进行零阶保持(zero-order hold)\(^{[8\hbox{-}9]}\), 产生图3连续限宽白噪声.
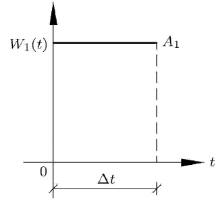
设连续限宽白噪声的分布为\(W(t)\), 其中离散的高斯分布为\( \underline{W} (t)\) (见图4), 每个阶梯的分布为\(W_i(t)\), \(t\)为在该阶梯横坐标范围内均匀分布的随机变量, \(W_i (t)\)为恒值. 例如将上图中第1个\(\Delta t\)范围取出.对于\(W_1 (t)\), \(t\)为在\([0, \Delta t)\)上均匀分布的随机变量, \(W_1 (t)\)恒等于\( {A}_1 \)(如 图4). 若令\(t_i = (i - 1)\Delta t\), 则\(W(t_i ) =\underline{W}(t)\), 为高斯分布\(N(0, \sigma ^2)\). 令\(W_i (t) = A_i \).下面对信号的自相关函数与功率谱密度函数进行推导.
当\(0 \leqslant \tau \leqslant \Delta t\), \(\underline{W}(t)\)的自相关函数为\[ \begin{array}R_{WW} (\tau ) = E[W(t)W(t + \tau )] =\Big (1 - \dfrac{\tau }{\Delta t} \Big)\sigma ^2 \end{array} \ \ (5)\]
当\( - \Delta t \leqslant \tau < 0\), 类似地, \(\underline{W} (t)\)的自相关函数为
\[ \begin{array}R_{WW} (\tau ) = E[W(t)W(t + \tau )] = \dfrac{1}{N}\sum_{i = 1}^N \Big (\dfrac{1}{\Delta t}\int_0^{\Delta t +\tau } W_i (t)W_i (t + \tau ) d t \Big )= \Big(1 + \dfrac{\tau }{\Delta t} \Big )\sigma ^2 \end{array} \ \ (6)\]
当\(\tau \in ( - \infty , \Delta t) \cup (\Delta t, + \infty )\):
已知对理想白噪声, 有\(R_{WW} (\tau ) = 2\pi S_0 \delta (\tau )\), 故\(R_{WW} (\tau \ne 0) = 0\).对于\(\underline{W}(t)\), \(\tau \in ( - \infty , \Delta t) \cup (\Delta t, + \infty )\)类似于理想白噪声的\(R_{WW} (\tau \ne 0)\).此时\(\underline{W}(t)\)的自相关函数为:\(R_{WW} (\tau ) = 0\).总而言之, 对于\(\underline{W} (t)\)
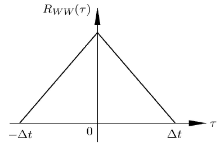
\[R_{WW} (\tau ) = \left\{ \!\!\begin{array}{l} \sigma ^2\Big(1 - \dfrac{ | \tau |}{\Delta t} \Big) \, , \ \ \tau \in [ - \Delta t, \Delta t] \\ 0\, , \ \ \tau \in ( - \infty , \Delta t) \cup (\Delta t, + \infty )\end{array} \!\!\right. \ \ (7)\]自相关函数图形见图5所示.
由维纳-辛钦公式, 对于自相关函数\(R_{WW} (\tau )\), 当\(\tau = 0\)时
\[ S_{WW} (\omega ) = \dfrac{1}{2\pi }\int_{ - \infty }^\infty {R_{WW} (\tau )} {\rm e}^{ -{\rm j}\omega t}d\tau =\\ \qquad \dfrac{\Delta t\sigma ^2}{2\pi }\left( {\dfrac{\sin ( {\omega \Delta t}/{2})}{{\omega \Delta t}/{2}}} \right)^2 \ \ (8)\]式(8)中功率谱密度函数见图6所示. 一般有[9]
\[S_0 = S_{WW} (0) = {\Delta t\sigma ^2}/(2\pi ) \ \ (9)\]
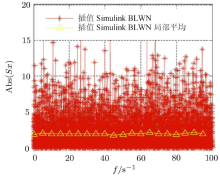
利用Matlab进行连续白噪声模型的模拟:在利用高斯分布生成限宽白噪声信号后, 对信号进行零阶保持, 以模拟信号点之后的均匀分布.图7展示了白噪声信号的分布状态; 图8将图7中椭圆区域放大, 展示了利用时域信号点插值形成的近似零阶保持的效果, 或近似的均匀分布; 图9显示了当时域信号点每次插值10段时, 信号的单边功率谱密度分布, 以及相应地局部平均后的幅值分布, 该分布与图7中连续白噪声功率谱密度函数的理论分布一致; 图10显示了当时域信号点不插值时, 信号的单边功率谱密度分布, 以及相应地局部平均后的幅值分布, 此时与图3 中的信号频域分布一致.
对于环境激励下复杂结构的响应分析, 利用限宽白噪声激振手段获取准确的响应幅值估计是较为困难的. 如果使用理想白噪声模型, 利用李雅普诺夫方程求解结构响应的协方差矩阵[10], 可以很方便地得到白噪声激励下结构的振动信号的方差, 从而估计结构的响应水平.本节以基底输入白噪声激励的三层剪切框架(见图11)为例, 利用理想白噪声模型和李雅普诺夫方程求取框架顶层的相对位移及 绝对加速度响应的理论方差值, 并与数值仿真结果进行对比.
结构的质量矩阵\({\pmb M}\)与刚度矩阵\({\pmb K}\)分别为\[{\pmb M} = \left[ \!\! \begin{array}{ccc} {m_1 } & 0 & 0 0 & {m_2 } & 0 0 & 0 & {m_3 }\end{array} \right] {\pmb K} = \left[\!\! \begin{array}{ccc} {k_1 + k_2 } & { - k_2 } & 0 { - k_2 } & {k_2 + k_3 } & { - k_3 } 0 & { - k_3 } & {k_3 }\end{array} \right] \]结构运动方程为\[{\pmb M}\ddot{\pmb x} + {\pmb C}\dot{\pmb x} + {\pmb K}{\pmb x} = - {\pmb M}\ddot{\pmb u}_{\rm g} \ \ (10)\]式中, \({\pmb x}\)为结构各层相对位移, \(\ddot{\pmb u}_{\rm g}\)为基底激励输入.令状态向量为\({\pmb y} = \left[\!\! \begin{array}{c} {{\pmb x}(t)_{3\times 1} } {\dot{\pmb x}(t)_{3\times 1} }\end{array}\!\! \right]\), 输入向量为\({\pmb w}(t) = \ddot{\pmb u}_{\rm g} (t)\), 构造状态方程\[\dot{\pmb y} ={\pmb A}{\pmb y} + {\pmb B}{\pmb w} \ \ (11)\]式中, 系统矩阵\({\pmb A}\)与控制矩阵\({\pmb B}\)分别为\[{\pmb A }= \left[\!\! \begin{array}{cc} { {\pmb O}_{3\times 3} } & { {\pmb I}_{3\times 3} } { - {\pmb M}^{ - 1}{\pmb K}} & { - {\pmb M}^{ - 1}{\pmb C}}\end{array} \!\! \right]\, {\pmb B} = \left[ \begin{array}{c} { {\pmb O}_{3\times 1} } { - 1} { - 1} { - 1}\end{array} \right]\]式(11)左右同乘以\({\pmb y}^{\rm T}\)有\[\dot{\pmb y}{\pmb y}^{\rm T} = {\pmb A}{\pmb y}{\pmb y}^{\rm T} + {\pmb B}{\pmb w}{\pmb y}^{\rm T} \ \ (12)\]求其期望\[ \begin{array}{l} E[ \dot{\pmb y}{\pmb y}^{\rm T}] = E[ A{\pmb y}{\pmb y}^{\rm T}] + E[ B{\pmb w}{\pmb y}^{\rm T}] = A E[{\pmb y}{\pmb y}^{\rm T}] + B E[{\pmb w}{\pmb y}^{\rm T}] \end{array} \ \ (13)\]令\(\varGamma = E[{\pmb y}{\pmb y}^{\rm T}]\), 有\[\dfrac{d{\pmb\varGamma} }{d t} = d( E[{\pmb y}{\pmb y}^{\rm T}])= E[ \dot {\pmb y}{\pmb y}^{\rm T} + {\pmb y}\dot {\pmb y}^{\rm T}] \ \ (14)\]代入式(13)\[\dfrac{d{\pmb\varGamma} }{d t} = E[ \dot{\pmb y}{\pmb y}^{\rm T} + {\pmb y}\dot {\pmb y}^{\rm T}] = {\pmb A} E[{\pmb y}{\pmb y}^{\rm T}] + {\pmb B} E[{\pmb w}{\pmb y}^{\rm T}] + E[{\pmb y}{\pmb y}^{\rm T}]{\pmb A}^{\rm T} +E[{\pmb y}{\pmb w}^{\rm T}]{\pmb B}^{\rm T} = {\pmb A}{\pmb\varGamma} + {\pmb\varGamma}^{\rm T}{\pmb A}^{\rm T} + {\pmb B} E[{\pmb w}{\pmb y}^{\rm T}] + E[{\pmb y}{\pmb w}^{\rm T}]{\pmb B}^{\rm T} \ \ (15)\]
已知结构状态向量\({\pmb y}\)在零初值下的积分解\[{\pmb y} = \int_0^t {\rm e}^{{A}(t - \tau )} {\pmb B}{\pmb w}(\tau )d\tau \ \ (16)\]因此有\[ E[ {\pmb w}(t) {\pmb y}^{\rm T}(t)] = E[{\pmb w} (t)\int _0^t {{\pmb w}^{\rm T}(\tau )} {\pmb B}^{\rm T}{\rm e}^{{A}^{\rm T}(t - \tau )}d \tau ] =\ \ E[ \int _0^t {{\pmb w} (t) {\pmb w}^{\rm T}(\tau )} {\pmb B}^{\rm T}{\rm e}^{{A}^{\rm T}(t - \tau )}d \tau ] =\ \ \int _0^t {E[{\pmb w} (t) {\pmb w}^{\rm T}(\tau )} ] {\pmb B}^{\rm T}{\rm e}^{{A}^{\rm T}(t - \tau )}d \tau \ \ (17)\]由于\({\pmb w} (t)\)为理想白噪声, 参考式(1), 有\[E[{\pmb w} (t) {\pmb w}^{\rm T}(\tau )] = 2\pi S_0 \delta (\tau - t) \ \ (18)\]故\[\begin{array}{c} E[{\pmb w} (t) {\pmb y}^{\rm T}(t)] =\ \ E \Big[ \int _0^t {2\pi S_0 } \delta (\tau - t) {\pmb B}^{\rm T}{\rm e}^{{A}^{\rm T}(t - \tau )} d \tau \Big] =\ \ E[ \pi S_0 {\pmb B}^{\rm T}] = \pi S_0 {\pmb B}^{\rm T} \end{array} \ \ (19)\]
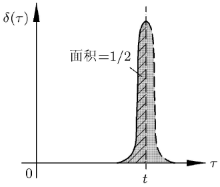
注意, 上式积分过程中, \(\int _0^t {f(\tau )\delta (\tau - t)} d(\tau ) =\dfrac{1}{2}f(t)\), 其原因在于\(\delta (\tau - t)\)处于积分右边界上, \(\delta(\tau - t)\)的积分只能计入一半的范围, 见图12所示.
代入式(15), 有\[ \dfrac{d{\pmb\varGamma} }{d t} = {\pmb A}{\pmb\varGamma} + {\pmb\varGamma}^{\rm T}{\pmb A}^{\rm T} + \pi S_0{\pmb B}{\pmb B}^{\rm T} + \pi S_0 {\pmb B}{\pmb B}^{\rm T}= {\pmb A}{\pmb\varGamma} +{\pmb\varGamma}^{\rm T}{\pmb A}^{\rm T} + 2\pi S_0 {\pmb B}{\pmb B}^{\rm T} \ \ (20)\]
对于时不变系统, 有\[\dfrac{d{\pmb\varGamma}}{d t} = {\bf 0} \ \ (21)\]
故\[{\pmb A}{\pmb\varGamma}+{\pmb\varGamma}^{\rm T}{\pmb A}^{\rm T} + 2\pi S_0 {\pmb B}{\pmb B}^{\rm T} = {\bf 0} \ \ (22)\]
满足李雅普诺夫方程. 注意到李雅普诺夫方程中未考虑观测矩阵, 求出的结果直接为状态向量的统计值. 为得到期望输出的方差估计, 需要在结果中增加相应的观测矩阵\({V}\)
\[{\pmb\varSigma} ={\pmb V}{\pmb\varGamma }{\pmb V}^{\rm T} \ \ (23)\]
对于本算例, 希望估计顶层的相对位移与绝对加速度的方差值, 观测矩阵、转换矩阵(用于在3个自由度的位移、加速度的估计值中提取第3层的数据)、方差估计分别为\[{\pmb V} = \left[ \!\!\begin{array}{cc} { {\pmb I}_{3\times 3} } & { {\pmb O}_{3\times 3} } { - {\pmb M}^{ - 1}{\pmb K}} & { - {\pmb M}^{ - 1}{\pmb C}}\end{array}\!\! \right]_{6\times 6} {\pmb T} = \left[\!\!\begin{array}{cccccc} 0 & 0 & 1 & 0 & 0 & 0 0 & 0 & 0 & 0 & 0 & 1 \end{array}\!\!\right] {\pmb\varSigma} = ({\pmb T}{\pmb V}) {\pmb \varGamma} ({\pmb T}{\pmb V})^{\rm T} \]
令算例中的参数取值为
\[ m_1 = m_2 = m_3 = 1\, 000\, {\rm kg}\\k_1 = k_2 = k_3 = 200\, {\rm MN} \\ {\pmb C} = 0.2 {\pmb M}+ 0.002 {\pmb K} \]
限宽白噪声的功率谱密度\(S_0 = 1\); 代入式(22)和式(23), 得\[{\pmb\varSigma} = \left[ \!\!\begin{array}{cc} {0.42} & {-17.06} \ { - 17.06} & {761.20}\end{array} \right]\]
可知顶层相对位移与绝对加速度的方差值分别为0.42与761.20, 注意该结果是在理想白噪声模型下得到的, 是理论解. 利用MatlabSimulink工具箱, 以及BLWN限宽白噪声工具, 进行信号模拟. 信号采样频率为1 000Hz, 信号时长为10 000s, 可得到结构顶层位移与加速度响应信号. 之后求取信号的协方差矩阵, 即得到顶层相对位移与绝对加速度的信号方差值\[{\pmb\varSigma} _{\rm Simulink} = \left[\!\! \begin{array}{cc} { 0.42} & { - 16.99} { - 16.99} & { 757.75}\end{array} \right]\]
由于结构为线性系统, 顶层响应同样也为白噪声. 对于顶层绝对加速度响应, 利用\(S_0 = \dfrac{\sigma ^2_{\rm s}}{2\pi f}\), 可求得信号的功率谱密度为0.12.也就是说, 对算例中的三层剪切框架, 功率谱密度为1的白噪声基底加速度, 可激励起结构顶层0.12的加速度响应.数值仿真的结果 与利用理想白噪声模型和李雅普诺夫方程计算的理论解十分接近.当降低信号采样频率, 或减少信号时长时, 数值计算的结果与理论值相比会有一定的误差. 注意在Matlab Simulink BLWN的设置中, 噪声为\(2\pi S_0 \).
调频质量阻尼器(tuned mass damper, TMD)通常简化称为TMD系统, 其由质量、弹簧、阻尼器构成, 通过改善结构共振特性来减振.自1909年Frahm首次提出后已在减振结构中广为应用\(^{[11\hbox{-}12]}\).本节以广州新电视塔TMD系统为研究对象, 利用随机地震金井清模型\(^{[13\hbox{-}14]}\)对结构及TMD系统的响应统计进行分析, 并对TMD系统进行参数优化. 结构模型选已标定的38节点模型[15](见图13), 其中1号节点嵌固于地面, 1\(\sim\)27单元为塔体, \n 28\(\sim \)37单元为天线桅杆.每个节点有5个自由度(依次为2个平动、3个转动), 结构共185个自由度, 其质量、阻尼、刚度阵分别为\({\pmb M}\), \({\pmb C}\), \({\pmb K}\). TMD系统安装于塔体顶层, 即第28个自由度. TMD系统为2个600\, t (\(m_{\rm TMD}\))的消防水箱, 设计TMD弹簧刚度\(k_{\rm TMD} = 541\)\, kN/m, 阻尼系数\(c_{\rm TMD} = 2.04\times 10^5\). 本节仅讨论结构\({\pmb x}\)向平动.
构造结构与TMD系统整体的质量阵\(\bar {\pmb M}\)、阻尼阵\(\bar {\pmb C}\)、刚度阵\(\bar {\pmb K}\), 有\[ \bar {\pmb M} = \left[ \!\! \begin{array}{cc} {\pmb M} & {\bf 0} \ {\bf 0 } & {\pmb m}_{\rm TMD }\end{array} \!\! \right]\]
$$ \bar {\pmb C} = \left[\!\! \begin{array}{cc} \left[\!\! \begin{array}{ccc} \cdots & \cdots & \cdots \\ \cdots & { \cdots + c_{\rm TMD} } & \cdots \\ \cdots & \cdots & \cdots\end{array} \!\! \right]_C & \begin{array}{c} \vdots \\ { - c_{\rm TMD } } \\ \vdots \end{array} \\ \begin{array}{ccc} \cdots & - c_{\rm TMD } & \cdots\end{array} & c_{\rm TMD } \\\end{array} \right]$$
\[ \bar {\pmb K} = \left[\!\!\begin{array}{cc} \left[\!\!\begin{array}{ccc} \cdots & \cdots & \cdots \\ \cdots & \cdots + k_{\rm TMD } & \cdots \\ \cdots & \cdots & \cdots\end{array} \!\! \right]_K & \begin{array}{c} \vdots \\{ - k_{\rm TMD } } \\ \vdots\end{array} \\ \begin{array}{ccc} \cdots & { - k_{\rm TMD} } & \cdots\end{array} & {k_{\rm TMD } } \end{array} \right]\]
\(\bar{\pmb C}\)和\(\bar{\pmb K}\)中省略号表示不含TMD系统的原结构阻尼和刚度阵的参数, 在此省略.金井清模型基岩加速度为\(\ddot {\pmb U}\). 地表土层相对加速度为\(\ddot {\pmb x}_{\rm g} \), 绝对加速度 为\(\ddot{\pmb u}_{\rm g} \)
\[\ddot {\pmb u}_{\rm g} = \ddot {\pmb x}_{\rm g} + \ddot {\pmb U} = - (2\zeta _{\rm g} \omega _{\rm g}\dot{\pmb x}_{\rm g} - \omega _{\rm g}^2 {\pmb x}_{\rm g} )\]
式中取\(\omega _{\rm g} = 4.5\)\, rad/s, \(\zeta _{\rm g}= 0.1\), 为软土地基.结构整体的运动方程\[\bar{\pmb M}\ddot{\pmb x} + \bar{\pmb C}\dot{\pmb x} + \bar{\pmb K}{\pmb x} = - \bar {\pmb M}{\pmb L}\ddot{\pmb u}_{\rm g} \ \ (24)\]
式中\({\pmb L}\)为单位阵, 提取结构\({\pmb x}\)向的平动自由度. 构造状态向量与状态方程
\[{\pmb y} = \left[ {\pmb x} \ \ {{\pmb x}_{\rm g} } \ \ \dot {\pmb x} \ \ {\dot{\pmb x}_{\rm g} } \right]^{\rm T}\ \ (25)\]
\[\dot {\pmb y} = {\pmb A}{\pmb y} + {\pmb B}{\pmb w}\ \ (26)\]
式中
\[{\pmb A} = \left[ \begin{array}{cccc}{\bf 0} & {\bf 0} & {\bf 1} & {\bf 0} \\ 0 & 0 & 0 & 1 \\ { - \bar {\pmb M}^{ - 1}\bar{\pmb K}} & {\omega _{\rm g}^2 \cdot {\pmb I}} & { -\bar {\pmb M}^{ - 1}\bar {\pmb C}} & { - 2\zeta _{\rm g} \omega _{\rm g} \cdot {\pmb I}} \\ 0 & { - \omega _{\rm g}^2 } & 0 & {2\zeta _{\rm g} \omega _{\rm g} } \end{array} \right]\]
\[{\pmb B} = \left[ {\bf 0} \ \ 0 \ \ {\pmb L} \ \ { - 1} \right]^{\rm T} \]
\({\pmb w}\)为白噪声, 功率谱密度\(S_0 = 1\).同上节, 令\({\pmb\varGamma} = E[ {\pmb y}{\pmb y}^{\rm T}]\), 则有\[{\pmb A}{\pmb \varGamma} + {\pmb \varGamma}^{\rm T}{\pmb A}^{\rm T} + 2\pi S_0 {\pmb B}{\pmb B}^{\rm T} = {\bf 0} \ \ (27)\]
提取结构及TMD系统的相对位移(相对地面)方差、绝对加速度方差进行响应分析. 以塔体(不包括天线桅杆)顶层相对位移标准差为控制目标, 对TMD参数进行敏感性分析, 见图14所示.图中, 横坐标为TMD阻尼比, 纵坐标为TMD自振频率与塔体1阶自振频 率之比. 图中横向虚线自下向上分别表示结构1\(\sim\)10阶自振频率, 横向点划线表示塔体设计TMD频率所在位置. 可以看出, 设计TMD的频率基本处于对塔体顶层位移的最优控制范围.
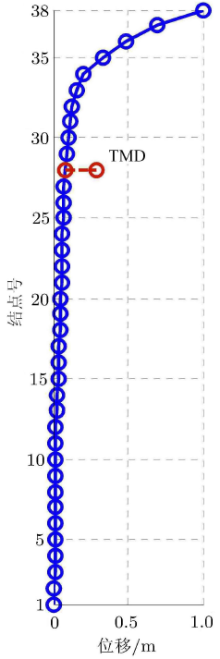
仍然以塔体顶层相对位移为控制目标, 利用约束置信域优化方法对TMD参数进行优化计算, 得到最优的参 数为\(k_{\rm TMD} = 554\)\, kN/m, 阻尼比\(\zeta _{\rm TMD}= 0.088\) (或阻尼系数\(c_{\rm TMD} = 1.43\times 10^5\)). 此时塔体及TMD系统的整体位移状态见图15所示.与TMD系统的设计参数(主要针对风载荷激励进行优化)相比, 刚度参数较为近似, 阻尼有一定差别.与文献[16]相比, 本文优化刚度更接近实际取值(弱轴方向), 且二者均存在对天线振动控制不佳的现象; 与文献[17]相比, TMD在地震作用下优化计算得到的阻尼比接近.另一方面, 相对时程分析方法, 随机振动方法计算速度更快, 在复杂结构的质量调谐阻尼器的参数优化中可凸显其计算效率高的优点.
本文对理想白噪声模型与限宽白噪声模型的模型概念、时频特征等进行了详细分析讨论, 其中包括信号的自相关函数与功率谱密度函数分布、信号的水平和带宽控制等. 对于连续系统, 推导了连续限宽白噪声的自相关函数分布, 并利用数值仿真对信号的频域特征进行了近似实现. 详细推导了利用李雅普诺夫方程与理想白噪声模型预测结构振动信号的方差特性的方法, 并结合三层框架进行了算例展示. 结合广州新电视塔及其TMD系统, 对利用随机振动方法进行结构控制优化设计的问题进行了研究. 本文为结构振动分析中的白噪声模型的使用提供了较为完整的理论思路.
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|