考虑温度影响的软黏土流变固结模型及解析解

引用本文

郭华, 刘干斌, 薛传成. 考虑温度影响的软黏土流变固结模型及解析解. 力学实践, 2018,40(1): 24-29
GUO Hua, LIU Ganbin, XUE Chuancheng. A RHEOLOGICAL CONSOLIDATION MODEL FOR SOFT CLAY WITH CONSIDERATION OF TEMPERATURE AND THE ANALYTICAL. MECHANICS IN ENGINEERING, 2018,40(1): 24-29. 复制到剪切板

Doi: 10.6052/1000-0879-17-346
Permissions

考虑温度影响的软黏土流变固结模型及解析解

郭华, 刘干斌, 薛传成

宁波大学岩土工程研究所, 浙江宁波 315211

作者简介：郭华,硕士研究生,主要从事多物理场土力学、软土地基处理方面的研究工作. E-mail：573860762@qq.com

收稿日期: 2017-11-11

资助项目: 国家自然科学基金资助项目(51478228).

摘要

基于四元件流变模型,考虑温度影响,建立了宁波软黏土流变固结模型,并利用拉普拉斯变换得到瞬时加载条件下的考虑温度影响的饱和软黏土流变固结解析解;利用不同温度下软黏土的流变固结试验结果,拟合获得了四元件流变模型参数,进行编程得到理论值, 并与试验值进行对比. 结果表明：该模型能较好反映宁波软黏土流变固结特性,计算结果与试验结果较为吻合.温度的升高导致渗透系数增大,在相同的时间内孔压消散越快, 固结越快.

关键词: 四元件模型; 温度; 流变固结解析解

中图分类号:TU4 文献标志码:A

A RHEOLOGICAL CONSOLIDATION MODEL FOR SOFT CLAY WITH CONSIDERATION OF TEMPERATURE AND THE ANALYTICAL

GUO Hua, LIU Ganbin, XUE Chuancheng

Institute of Geotechnical Engineering, Ningbo University, Ningbo 315211, Zhejiang, China

Abstract

Based on the four element rheological model, a rheological consolidation model for the Ningbo soft clay is established with consideration of the influence of temperature, and the analytical solution for the rheological consolidation of the saturated soft clay under instantaneous loading conditions is obtained by Laplace transform. Based on the rheological consolidation test results of soft clay in different temperatures, the parameters in the rheological Ningbo soft clay four element model are determined. And the theoretical values are compared with the experimental values. It is shown thatthe model can well reflect the rheological consolidation characteristics of the Ningbo soft clay,and the calculated results are in good agreement with the experimental results. The increase of the temperature leads to an increase of the permeability coefficient, and the pore pressure dissipates at the same time, leading to an accelerated consolidation.

Key words: four component model; temperature; analytical solution of rheological consolidation

文章图片

饱和软黏土的沉降不仅和载荷有关, 还和时间、温度的影响有关, 土体在载荷的长期时间效应下会产生土体沉降量以及土体强度随时间而改变的现象, 即为土体的流变.

一些学者针对不同地区的软黏土流变特性进行了温控固结试验和理论、土体流变理论等方面的研究.Delage等^[1]研究了饱和土的热固结多场耦合作用的问题, 将爆炸黏土的温度从20$^{\circ}$C上升到90$^{\circ}$C, 发现其渗透系数增大.白冰等^[2]对饱和粉质黏土进行了热固结特性试验, 结果表明：温度升高导致孔压增大, 固结排水量远大于温度再降低后的吸水量, 土样总变形量增大. 邵玉娴等^[3]针对南京3种黏土进行了5$^{\circ}$C $\sim$50$^{\circ}$C条件下的吸水量、渗透性和膨胀性等试验, 结果表明渗透系数随温度升高而上升10倍, 深入揭示了黏性土水理性质的温度规律. 吴瑞潜^[4]从传统固结、热弹性、渗流、热传导理论出发, 推导出了应力场、渗流场、温度场控制方程, 并根据不同工况做了简化, 建立饱和土体一、二、三维热固结方程.陈迪等^[5]针对了无限长圆柱的热固结问题, 考虑热渗效应和热流固耦合效应建立了饱和土体的热固结问题解析解, 分析了非等温情况下热渗系数和固结系数对土体固结度和孔压变化的影响.Laloui等^[6]针对热硬化在内的各向同性的热应力路径, 基于孔隙率会随温度变化, 提出了一种新的热塑性机制, 建立了Thermo Cam-clay模型.

根据国内外学者的研究, 土体流变模型分为两大类：线性流变模型、非线性流变模型. 谢新宇等^[7]采用西元模型对一维固结流变试验和三轴流变试验结果进行了分析, 并扩展到三维情况, 对三轴流变试验结果进行拟合确定模型参数.邓宗伟等^[8]对西元模型低应力分量进行了分析和改进得到了改进的一维固结解析解, 并将其应用于软土路堤试验沉降计算, 因此在计算沉降时不仅要考虑不同应力水平还要考虑软土流变的滞后效应.Li等^[9]根据饱和软黏土流变固结考虑了Hansbo渗流模型和简化形式, 指出非达西渗流导致现实情况中流变固结沉降速度小于理论值.郑榕明等^[10]同时考虑淤泥质黏土的弹性流变和塑性流变效应, 根据土体蠕变试验结果提出了非线性黏塑性流变模型, 并对上海地铁一深基坑进行了数值分析.王宏贵等^[11]将一维的西元模型应力应变扩展到三维情况, 根据竖向应变方程对长期单向压缩试验结果进行曲线拟合确定了流变模型的本构参数.Xie等^[12]考虑到不同的加荷方式, 利用三元件模型计算出循环载荷作用下的一维黏弹性固结解.李西斌^[13]针对萧山软土线性流变模型提出了一种线性流变固结模型参数非线性拟合方法, 计算的沉降值与实际值很接近.

在传统的四元件流变模型基础上, 考虑温度对渗透系数的影响, 建立了温度作用下的软黏土一维流变固结理论, 并针对宁波软黏土进行温控流变固结试验, 根据试验结果对该理论进行自定义编程拟合模型参数, 能够较好反映温度影响下宁波软黏土流变固结特性.

1 考虑温度影响的流变固结方程

1.1 四元件流变模型

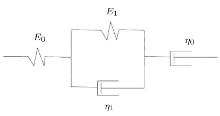
传统四元件流变模型如图1所示. 该模型由一个弹性模量为$E_0 $的弹簧、一个黏滞系数为$\eta _0$的黏壶和一个开尔文体串联而成. 开尔文体由一个弹性模量为$E_1 $的弹簧、一个黏滞系数为$\eta _1 $的黏壶并联而成.

	Figure Option View Download New Window
	图 1 四元件模型

1.2 流变固结方程

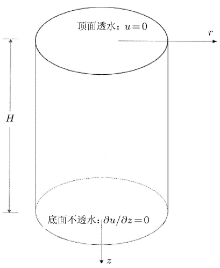
对于单层地基固结, 假设软黏土层厚度为$H$, 地面作用随时间变化的连续均布载荷$q(t)$, 竖向渗透系数$k_{Tv}$是一个随温度变化的一次函数, 单面排水情况如图2所示.

	Figure Option View Download New Window
	图 2 单面排水

忽略温度对土骨架的变形, 即不考虑温度对元件参数的影响, 由四元件模型, 可得土体应力-应变关系\[\varepsilon _z = \dfrac{\sigma'_z }{E_0 } + \int_0^t {\dfrac{\sigma'_z }{\eta _0 }} d\tau + \int_0^t{\dfrac{\sigma'_z }{\eta _1 }} {\rm e}^{ - \tfrac{E_1 }{\eta _1 }(t - \tau )} d\tau \ \ (1)\]式中, $\sigma'_z $为竖向有效应力; $\varepsilon _z $为竖向应变; $E_0 $, $\eta _0 $, $E_1 $, $\eta _1$为四元件模型参数.

由有效应力原理, 可得\[\sigma'_z = q(t) - u \ \ (2)\]式中, $q(t)$为作用在土体上随时间变化的载荷, $u$为孔隙水压力.

饱和土体单位时间内排出的水量等于土骨架的压缩量, 可得\[\dfrac{k_{Tv} }{\gamma _{\rm w} }\dfrac{\partial ^2u}{\partial z^2} = - \dfrac{\partial \varepsilon _z}{\partial t} \ \ (3)\]式中, $k_{Tv} $为温度影响下的土体竖向渗透系数, $\gamma _{\rm w} $为土中水的重度.

将式(1), 式(2)代入式(3), 得到饱和软黏土一维流变固结方程\[\begin{array} c_{Tv} \dfrac{\partial ^2u}{\partial z^2} = \dfrac{\partial u}{\partial t} +\dfrac{E_0 }{\eta _1 }\int_0^t {\dfrac{\partial u}{\partial \tau }} {\rm e}^{ - \tfrac{E_1 }{\eta _1 }(t -\tau )} d\tau +\\ \qquad \dfrac{E_0 }{\eta _0 }u - \dfrac{ d q(t)}{d t} -\dfrac{E_0 }{\eta _0 }q(t)-\\ \qquad \dfrac{E_0 }{\eta _1 }\int_0^t {\dfrac{d q(\tau )}{d\tau }} {\rm e}^{ - \tfrac{E_1 }{\eta_1 }(t - \tau )} d\tau \end{array} \ \ (4)\]式中, $c_{Tv} $是土体的竖向固结系数, $c_{Tv} = \dfrac{k_{Tv} E_0 }{\gamma _{\rm w}}$.

由于水的黏滞系数和温度有关^[14], 在一个标准大气压下, 水的黏滞性系数和温度关系如表1所示.

表 1 不同温度下水的黏滞系数

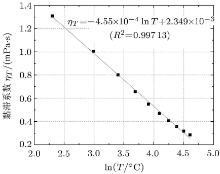
将上述表中温度和黏滞系数的关系做拟合曲线, 如图3所示.

	Figure Option View Download New Window
	图3 温度和黏滞系数拟合关系

根据上述温度和黏滞系数的关系, 可得拟合关系式\[\eta _T = - 0.455\times 10^{ - 3}{\rm ln} T + 2.349\times 10^{ - 3} (R^2 = 0.997) \ \ (5)\]

因为土体黏滞系数和土骨架的渗透率和渗透系数等有关, 其关系式如下\[k_{Tv} = \dfrac{\kappa \rho _{\rm w} g}{\eta _T } \ \ (6)\]式中$\kappa $是渗透率, $\rho_{\rm w}$为水的密度, $g$为重力加速度.

由式(5)和式(6), 可得温度和渗透系数的关系式\[k_{Tv} = \dfrac{\kappa \rho _{\rm w} g}{ - 4.54\times 10^{-4} {\rm ln} T + 2.349\times 10^{ - 3}} \ \ (7)\]

由式(4)和式(7), 可得温度影响的饱和软黏土一维流变固结控制方程如下 \[\dfrac{k_{Tv} E_0 }{\gamma _{\rm w} }\dfrac{\partial ^2u}{\partial z^2} = \dfrac{\partial u}{\partial t} + \dfrac{E_0 }{\eta _1 }\int_0^t {\dfrac{\partial u}{\partial \tau }} {\rm e}^{ - \tfrac{E_1 }{\eta _1 }(t - \tau )} d\tau + \dfrac{E_0 }{\eta _0 }u + f(t)\ \ (8)\]

$$f(t) = - \dfrac{d q(t)}{d t} - \dfrac{E_0 }{\eta _0 }q(t) - \dfrac{E_0 }{\eta _1 }\int_0^t{\dfrac{d q(\tau )}{d\tau }} {\rm e}^{ - \tfrac{E_1 }{\eta _1 }(t - \tau )} d\tau \ \ (9)$$

2 方程求解

外载荷加载形式复杂, 初始载荷为瞬时加载, 其大小为$q_0 $, 则上述控制方程简化为

\[ \dfrac{k_{Tv} E_0 }{\gamma _{\rm w} }\dfrac{\partial ^2u}{\partial z^2} =\dfrac{\partial u}{\partial t} + \dfrac{E_0 }{\eta _1 }\int_0^t {\dfrac{\partial u}{\partial \tau }}{\rm e}^{ - \tfrac{E_1 }{\eta _1 }(t - \tau )}d\tau + \dfrac{E_0 }{\eta _0 }u - \dfrac{E_0 }{\eta _0 }q_0\ \ (10)\]边界条件：对于单面排水的情况, $u(0, t) = 0$, $u_z (H, t) = 0$初始条件：$u({z}, 0) = q_0 $

由分离变量法得孔压$u$表达式为\[u(z, t) = \sum_{n = 1}^\infty {T_n (t)} \sin \Big(\dfrac{N}{H}z \Big) \ \ (11)\]

式中, $T_n (t)$是关于时间$t$的一次函数, $N = \dfrac{1}{2}(2n - 1)\pi $, $n = 1, 2, 3, \cdots$.

将式(11)代入控制方程(10), 可得方程如下 \[ \dfrac{k_{Tv} E_0 }{\gamma _{\rm w} }\dfrac{N^2}{H^2}T_n (t) + T'_n (t) + \dfrac{E_0 }{\eta_1 }\int_0^t {T'_n (\tau )} {\rm e}^{ - \tfrac{E_1 }{\eta _1 }(t - \tau )} d\tau + \dfrac{E_0 }{\eta _0 }T_n (t) - \dfrac{E_0 }{\eta _0 }\dfrac{2q_0 }{N} = 0 \ \ (12)\]

对式(12)进行拉普拉斯变换, 得\[ \begin{array}k_{Tv} \dfrac{N^2}{H^2}F_n (s) + sF_n (s) - T_n (0) +\dfrac{E_0 }{\eta _1 \Big(s + {E_1}/{\eta _1 }\Big)}[sF_n (s) - T_n (0)] + \dfrac{E_0 }{\eta _0 }T_n (t) + \dfrac{E_0 }{\eta _0}F_n (s) - \dfrac{E_0 }{\eta _0 }\dfrac{2q_0 }{Ns} = 0 \end{array} \ \ (13)\]

由初始条件, 可得\[F_n (s) = \dfrac{\dfrac{2q_0 }{N}\Big (\dfrac{E_0 }{s\eta _0 } + 1 + \dfrac{E_0 }{E_1 + \eta _1s}\Big)}{k_{Tv} \dfrac{N^2}{H^2} + \dfrac{E_0 }{\eta _0 } + s + \dfrac{E_0 s}{s\eta _1 + E_1 }} \ \ (14)\]

对上式进行拉氏逆变换, 可得时间参数\[ T_n (t) = {\rm L}^{ - 1}[F_n (s)] = \dfrac{2q_0 }{N}(D_1 {\rm e}^{x_1 T_V } - D_2 {\rm e}^{x_2 T_V } + C) \ \ (15)\]

将式(15)代入式(11), 可得孔压表达式\[u = q_0 \sum_{n = 1}^\infty \dfrac{2}{N}\sin\Big (\dfrac{N}{H}z\Big) (D_1 {\rm e}^{x_1 T_V } - D_2 e^{x_2T_V } + C) \ \ (16)\]式中, $N = \dfrac{1}{2}(2n - 1)\pi $, $n = 1, 2, 3, \cdots$, 系数$x_1 $, $x_2 $, $C$, $D_1 $, $D_2 $, $T_V$, $a_1 $, $a_2 $, $b$的表达式为\[\begin{array}{l} x_{1, 2} = - \dfrac{1}{2b} \Big[(1 + a_1 + a_2 + N^2b)\pm \\ \qquad \sqrt {(1 + a_1 + a_2 + N^2b)^2 - 4a_1 (a_2 + N^2b)} \Big] \\ C = \dfrac{a_2 }{a_2 + N^2b} , \ \ D_1 = \dfrac{N^2(bx_1 + a_1 )}{bx_1 (x_2 - x_1 )} \\ D_2 = \dfrac{N^2(bx_2 + a_1 )}{bx_2 (x_2 - x_1 )} , \ \ a_1 = \dfrac{E_1 }{E_0 } , \ \ a_2 = \dfrac{\eta _1 }{\eta _0 } \\ T_V = \dfrac{k_{Tv} E_0 t}{\gamma _{\rm w} H^2} =\dfrac{\kappa \rho _{\rm w} gE_0 t}{\gamma _{\rm w} ( - 0.454\times 10^{ -3}\ln T + 2.349\times 10^{ - 3})H^2} \\ b = \dfrac{k_{Tv} \eta _1 }{H^2\gamma _{\rm w} }=\dfrac{\kappa \rho _{\rm w} g\eta _1 }{( - 0.454\times 10^{ - 3}\ln T +2.349\times 10^{ - 3})H^2\gamma _{\rm w} } \end{array}\]

土层平均固结度公式如下\[\overline{U} = 1 - \dfrac{\int_0^H {ud z} }{\int_0^H {u_0 d z} } \ \ (17)\]

将式(16)代入式(17), 可得考虑温度影响的平均固结度表达式为\[\overline{U} = 1 - \sum_{n = 1}^\infty {\dfrac{2}{N^2}} (D_1 {\rm e}^{x_1 T_V } - D_2 {\rm e}^{x_2 T_V } + C)\ \ (18)\]

由考虑温度作用的渗透系数$k_{Tv} $可得参数$T_V$和$b$, 因此由式(16)和式(18)得到考虑温度影响的软黏土孔压和固结度关系式.

3 算例分析

3.1 模型参数

采用自行研制的温控三轴仪对宁波软黏土进行流变固结试验.温控系统采用弧形板加热器进行加热, 且加热功率可自行调节实现快速加热.加热器围绕压力室周围一圈, 可对土样均匀加热, 且温度控制器通过高精度温度传感器可实现对压力室内的温度进行精确控制和测量.

土样为宁波软黏土原状样, 土体直径39.1 mm, 高80 mm, 采用真空抽气饱和, 使其饱和度大于95%.试样采用分级加载方式, 分别在50 kPa, 100 kPa, 200 kPa和30$^{\circ}$C, 45$^{\circ }$C, 60$^{\circ }$C, 75$^{\circ }$C温度下进行温控固结试验.试验采用先加压后升温方式进行, 孔压稳定后进行排水固结, 持续加载至孔压消散95%时为止, 试验时长约5 h, 以固结试验数据来进行流变固结过程的拟合及分析.

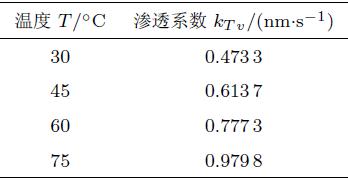
在常温下, 宁波软黏土渗透率$3.81\times 10^{ - 4}$ $\mu$m$^{2}$, 土骨架固有渗透率大小不随温度变化而改变.根据理论式(7), 代入渗透率参数和不同温度值, 可计算得到不同温度下的渗透系数, 如表2所示.

表 2 不同温度下的渗透系数

为得到四元件模型参数, 利用Origin软件对本文考虑温度影响的饱和软黏土一维流变固结方程来进行自定义拟合函数. 不考虑温度对元件参数的影响, 故对30$^{\circ}$C时不同固结压力下的土样孔压试验值进行非线性拟合, 只考虑不同温度下的渗透系数对孔压及土体沉降的影响, 得到自定义函数曲线, 即温度为30$^{\circ}$C 时土样固结压力分别为50 kPa, 100 kPa, 200 kPa的孔压试验值和拟合曲线, 如图4所示.

	Figure Option View Download New Window
	图 4 30$^{\circ}$C时不同固结压力下的孔压拟合曲线

图中以时间对数$\ln t$为横坐标, 孔压值为纵坐标.由图可知, 温度一定时, 固结压力越大, 孔压值越大; 孔压随时间对数增长而逐渐消散.当固结压力一定时, 孔压消散速度先增快后逐渐减慢.温度30$^{\circ}$C时四元件流变固结模型参数如表3所示, 表中$R^2$为拟合结果的相关系数.不同固结压力下拟合值和试验值吻合较好, 说明四元件模型参数取值较合理.

表 3 30$^{\circ}$C时不同固结压力下的四元件模型参数

3.2 考虑温度影响的流变理论值分析

为了研究温度作用下渗透系数的改变对一维流变固结理论的影响, 且忽略温度对元件模型参数的影响, 将渗透系数作为唯一的变量, 因此在不同固结压力下将得到的30$^{\circ}$C元件模型参数设为固定值, 利用Matlab软件进行编程计算, 得到不同温度下渗透系数改变所得的理论值.将理论值与试验值进行对比, 如图5所示.

	Figure Option View Download New Window
	图 5 不同温度下孔压理论值与试验值

由不同温度下的孔压理论值与试验值曲线可知, 固结压力一定时, 孔压随时间增大逐渐消散, 温度越高, 消散至相同孔压时所用的时间越短, 且在相同的时间内孔压消散得越快.温度升高导致渗透系数增大, 从而加快了孔压消散过程, 加快了排水固结, 和试验曲线趋势完全一致.但当温度为45$^{\circ}$C, 60$^{\circ }$C, 75$^{\circ}$C时, 理论值和计算值略有不同导致吻合度有所差别, 一方面是由于试验误差导致, 另一方面是因为温度不只影响了渗透系数, 还会对元件模型的参数取值产生一定影响. 元件参数的取值只影响孔压消散过程, 但不影响最终的消散结果.

4 结论

根据所建立的考虑温度影响的一维流变固结方程, 利用解析方法进行求解, 并对试验结果进行了对比, 主要结论如下：

(1) 在温控流变固结试验中, 固结占主导地位, 不同温度下的孔压消散试验值能够较好地反映宁波软黏土的流变规律.

(2) 当固结压力一定时, 随着温度的升高会导致渗透系数增大, 孔压消散越快, 固结越快.

(3) 温度影响下土体孔压试验值曲线和理论值曲线趋势完全一致.

(4) 试验值与理论值的差异主要是由于实验误差和四元件模型参数的取值引起的.

The authors have declared that no competing interests exist.

参考文献

文献选项

[1]	Delage P, Sultan N, Cui YJ, et al. Permeability changes in boom clay with temperature. Oai: arXir. org: 1112. 6396, 2011 [本文引用:1]
[2]	白冰, 陈星欣. 热-冷反复变化过程中饱和黏性土的热固结试验研究. 工程力学, 2011, 28(10): 139-144 [本文引用:1]
[3]	邵玉娴, 施斌, 刘春. 黏性土水理性质温度效应研究. 岩土工程学报, 2011, 33(10): 1576-1582 [本文引用:1]
[4]	吴瑞潜. 饱和土一维热固结解析理论研究. [博士论文]. 杭州: 浙江大学, 2008 [本文引用:1]
[5]	陈迪, 郑荣跃, 刘干斌. 考虑热渗效应的有限热源固结近似解. 力学与实践, 2016, 38(3): 294-298 [本文引用:1]
[6]	Laloui L, Cekerevac C. Thermo-plasticity of clays: an isotropic yield mechanism. Computers and Geotechnics, 2003, 30(8): 649-660 [本文引用:1]
[7]	谢新宇, 李金柱, 王文军. 宁波软土流变试验及经验模型. 浙江大学学报(工学版), 2012, 46(1): 64-71 [本文引用:1]
[8]	邓宗伟, 唐葭, 朱志祥. 基于改进西元模型的软土流变一维固结解析. 湖南大学学报(自然科学版), 2014, 41(6): 85-91 [本文引用:1]
[9]	Li CX, Wang KH. Analysis of 1D consolidation with non-Darcian flow described by exponent and threshold gradient. Journal of Zhejiang University-Science A(Applied Physics & Engineering), 2010, 11(9): 656-667 [本文引用:1]
[10]	郑榕明, 陆浩亮, 孙钧. 软土工程中的非线性流变分析. 岩土工程学报, 1996, 18(5): 1-13 [本文引用:1]
[11]	王宏贵, 魏丽敏, 贺晓光. 根据长期单向压缩试验结果确定三维流变模型参数. 岩土工程学报, 2006, 28(5): 669-673 [本文引用:1]
[12]	Xie KH, Xie XY, Li XB. Analytical theory for one-dimensional consolidation of clayey soils exhibiting rheological characteristics under time-dependent loading. International Journal for Numerical & Analytical Methods in Geomechanics, 2008, 32(14): 1833-1855 [本文引用:1]
[13]	李西斌. 线性流变固结模型参数的回归反演分析法. 南昌大学学报(工学版), 2012, 34(3): 233-238 [本文引用:1]
[14]	张国强. 流体力学. 北京: 机械工业出版社, 2006 [本文引用:1]

1112

0.0

... Delage等^[1]研究了饱和土的热固结多场耦合作用的问题,将爆炸黏土的温度从20$^{\circ}$C上升到90$^{\circ}$C,发现其渗透系数增大 ...

2011

0.0

白冰, 陈星欣. 热-冷反复变化过程中饱和黏性土的热固结试验研究. 工程力学, 2011, 28(10): 139-144

The thermal consolidation characteristics of saturated clay under cyclic heating and cooling are studied by laboratory tests. Test results show that the temperature rising ratio of specimens decreases with the increasing of temperature. However, the temperature dropping ratio is just contrary. Furthermore, the patterns of temperature variation of specimens during the period whether the processes of rising or cooling are independent of the cyclic number of thermal loading and confining pressure. An obvious pore pressure is generated by heating in undrained conditions. It should be pointed out that the pore pressure in the first number of cyclic thermal loading is much larger than that in the second number of cyclic thermal loading. On the other hand, a negative pore pressure is first induced by cooling in undrained conditions. Then, when the temperature is dropped to the required temperature value, the pore pressure begins to rise and subsequently becomes to be a positive pore pressure. Whether after the heating processes or after the cooling processes, a drainage effect of specimens is displayed generally in drained conditions. Furthermore, the volumetric strain induced by heating is much larger than that induced by cooling.

对热-冷反复变化过程中饱和粘性土的热固结特性进行了室内试验。试验表明，随着试样温度的升高，温度的上升速率逐渐减慢，而在降温过程中则正好相反。而且，温度变化过程与温度荷载循环次数、试样所受到的围压无关；不排水加热过程中会诱致显著的孔隙水压力，而第2个温度循环过程要比第1个温度循环过程诱致的孔隙水压力要小；在不排水温度下降过程中，试样内先产生负的孔隙水压力，当温度下降至设定的温度值后，孔隙水压力又开始上升，随后转化为正的孔隙水压力；如果允许试样排水(或吸水)，则试样在加热和降温后的等温过程一般表现为收缩排水过程，且加热后所引起的排水体应变要远大于降温后所引起的排水体应变。

... 白冰等^[2]对饱和粉质黏土进行了热固结特性试验,结果表明：温度升高导致孔压增大,固结排水量远大于温度再降低后的吸水量,土样总变形量增大 ...

2011

0.0

邵玉娴, 施斌, 刘春. 黏性土水理性质温度效应研究. 岩土工程学报, 2011, 33(10): 1576-1582

... 邵玉娴等^[3]针对南京3种黏土进行了5$^{\circ}$C $\sim$50$^{\circ}$C条件下的吸水量、渗透性和膨胀性等试验,结果表明渗透系数随温度升高而上升10倍,深入揭示了黏性土水理性质的温度规律 ...

2008

0.0

... 吴瑞潜^[4]从传统固结、热弹性、渗流、热传导理论出发,推导出了应力场、渗流场、温度场控制方程,并根据不同工况做了简化,建立饱和土体一、二、三维热固结方程 ...

2016

0.0

陈迪, 郑荣跃, 刘干斌. 考虑热渗效应的有限热源固结近似解. 力学与实践, 2016, 38(3): 294-298

摘　要：通过建立考虑热渗效应和热流固耦合效应的饱和土体固结方程,研究了无限长圆柱热固结问题.利用Fourier和Laplace变换及其逆变换,给出了热固结问题的解析解;然后对空间内无限长圆柱形热源问题进行研究,得到非等温条件下柱体周围饱和土体温度、孔隙水压力的近似解,并总结其规律,分析了热渗系数、固结系数对温度作用下土体固结的影响.

... 陈迪等^[5]针对了无限长圆柱的热固结问题,考虑热渗效应和热流固耦合效应建立了饱和土体的热固结问题解析解,分析了非等温情况下热渗系数和固结系数对土体固结度和孔压变化的影响 ...

2003

0.0

... Laloui等^[6]针对热硬化在内的各向同性的热应力路径,基于孔隙率会随温度变化,提出了一种新的热塑性机制,建立了Thermo Cam-clay模型 ...

2012

0.0

谢新宇, 李金柱, 王文军. 宁波软土流变试验及经验模型. 浙江大学学报(工学版), 2012, 46(1): 64-71

One-dimensional consolidation rheological tests and triaxial rheological tests were conducted in order to analyze the rheological characteristics and rheological model of Ningbo soft soil. The results of rheological tests showed that the process of rheology was weaken by the lateral confinement in consolidation rheological tests, and the equal-time stress-strain curves deviated to the stress axis; while in triaxial rheological tests, the process of rheology adequately developed, and the equal-time stress-strain curves deviated to the strain axis, which better revealed the rheological characteristics of soft soil. The stress-strain relationship of one-dimensional Nishihara model was extended to three-dimension, and the yield function of modified Cambridge model was used to describe the plastic yield property. The calculation formula of creep strain with const load was developed, with which the triaxial rheological tests datas of Ningbo soft soil were fitted, and the parameters of Nishihara model were determined. Results show that the model is suitable for the rheological law of Ningbo soft soil．

为了研究宁波软土的流变特性及经验模型,进行一维固结流变试验和三轴排水流变试验,并采用西原模型拟合模型参数.试验对比分析表明,固结试验的侧限作用会阻碍试样流变的发展,应力-应变等时曲线偏向应力轴,而三轴流变试验试样的流变能够得到充分地发展,应力-应变等时曲线偏向应变轴,能够更好地体现软黏土的流变性状.将一维西原模型应力-应变关系扩展到三维,采用修正剑桥模型屈服函数描述材料的塑性屈服.推导荷载恒定时土样的轴向应变计算公式,根据三轴排水流变试验结果进行曲线拟合,确定西原模型参数.结果表明,该模型能够较好地符合宁波软土的流变规律.

... 谢新宇等^[7]采用西元模型对一维固结流变试验和三轴流变试验结果进行了分析,并扩展到三维情况,对三轴流变试验结果进行拟合确定模型参数 ...

2014

0.0

邓宗伟, 唐葭, 朱志祥. 基于改进西元模型的软土流变一维固结解析. 湖南大学学报(自然科学版), 2014, 41(6): 85-91

摘　要：为解决不同应力水平下饱和软土层的沉降计算问题，考虑土的流变特性，对西原模型低应力分量进行了分析和改进．通过Laplace变换与反变换，得到了瞬时加载条件下改进西原模型的一维固结解析解，在此基础上采用积分的方法推导了多级加载条件下的统一解析解，并将解析解应用于洞庭湖软土路堤试验段的沉降计算．结果表明：该解析解沉降计算值在不同应力水平下呈现不同的变化规律，均与对应应力水平下的沉降实测值吻合．在固结初期，该解析解的计算固结沉降速率大大低于相同条件下弹性模型的计算结果．因此，在计算软基沉降时，必须考虑不同应力水平对软基沉降的影响，并考虑软土流变所引起的滞后效应．

... 邓宗伟等^[8]对西元模型低应力分量进行了分析和改进得到了改进的一维固结解析解,并将其应用于软土路堤试验沉降计算,因此在计算沉降时不仅要考虑不同应力水平还要考虑软土流变的滞后效应 ...

2010

0.0

... Li等^[9]根据饱和软黏土流变固结考虑了Hansbo渗流模型和简化形式,指出非达西渗流导致现实情况中流变固结沉降速度小于理论值 ...

1996

0.0

郑榕明, 陆浩亮, 孙钧. 软土工程中的非线性流变分析. 岩土工程学报, 1996, 18(5): 1-13

... 郑榕明等^[10]同时考虑淤泥质黏土的弹性流变和塑性流变效应,根据土体蠕变试验结果提出了非线性黏塑性流变模型,并对上海地铁一深基坑进行了数值分析 ...

2006

0.0

王宏贵, 魏丽敏, 贺晓光. 根据长期单向压缩试验结果确定三维流变模型参数. 岩土工程学报, 2006, 28(5): 669-673

The stress-strain relationship of the one-dimensional Xiyuan Model was developed into three-dimensional stress state.The visco-elastic plastic constitutive equation was applied in the model and its vertical strain expression was regarded as the fundamental equation to simulate the test data of the long term oedometer test to get the parameters of the rheological model.This method was very convenient and the physical meaning of the parameters obtained was clear.And the method could also be applied to determine the parameters of other rheological model.

将一维西原模型的应力–应变关系推广为三维应力状态的弹-粘弹-粘塑本构方程,以其竖向应变表达式作为基本方程,对长期单向压缩试验结果进行曲线拟合,从而确定该流变模型的本构参数。该方法简便快捷,所获参数物理意义明确,可推广应用于其它流变模型的参数确定。

... 王宏贵等^[11]将一维的西元模型应力应变扩展到三维情况,根据竖向应变方程对长期单向压缩试验结果进行曲线拟合确定了流变模型的本构参数 ...

2008

0.0

... Xie等^[12]考虑到不同的加荷方式,利用三元件模型计算出循环载荷作用下的一维黏弹性固结解 ...

2012

0.0

李西斌. 线性流变固结模型参数的回归反演分析法. 南昌大学学报(工学版), 2012, 34(3): 233-238

提出了一种精度高、应用方便的线性流变固结模型参数非线性拟合方法.利用大型数据处理软件origin7.5自定义函数二次开发功能,依据已有流变固结解析理论编制了相应的自定义拟合函数,并对5组萧山软土一维流变固结试验数据进行了回归分析,得到了三元件和四元件流变固结模型的参数,并分析了其变化规律.采用所得参数,利用解析理论计算了试样的沉降和超静孔压,并将理论计算所得沉降和孔压曲线与试验实测曲线进行了对比.结果表明:提出的拟合方法非常有效,拟合所得萧山软土线性流变模型参数有一定的规律,且按所得参数进行理论计算的沉降值与实测值非常吻合.

... 李西斌^[13]针对萧山软土线性流变模型提出了一种线性流变固结模型参数非线性拟合方法,计算的沉降值与实际值很接近 ...

2006

0.0

... 由于水的黏滞系数和温度有关^[14],在一个标准大气压下,水的黏滞性系数和温度关系如表1所示 ...

	Figure Option View Download New Window
	图 4 30\(^{\circ}\)C时不同固结压力下的孔压拟合曲线